The velocity of a body moving in a straight line is given by v=(3x2+x)m/s . Find acceleration at x=2m.
Video Solution
Text Solution
v=(3x2+x)
dvdx=6x+1
a=vdvdx=(32+x)(6x+1)
at x=2m
a=(3×22+2)(6×2+1)=182m/s2
|
Topper's Solved these Questions
- UNIT DIMENSION, VECTOR & BASIC MATHSBOOK - BANSALCHAPTER - UNIT DIMENSION, VECTOR & BASIC MATHSEXERCISE - PRACTICE EXERCISE
4 Videos
- UNIT DIMENSION, VECTOR & BASIC MATHSBOOK - BANSALCHAPTER - UNIT DIMENSION, VECTOR & BASIC MATHSEXERCISE - EXERCISE-1 [SINGLE CORRECT CHOICE TYPE]
20 Videos
- UNIT DIMENSION, VECTOR & BASIC MATHSBOOK - BANSALCHAPTER - UNIT DIMENSION, VECTOR & BASIC MATHSEXERCISE - Exercise
10 Videos
- KINETIC THEORY OF GASESBOOK - BANSALCHAPTER - KINETIC THEORY OF GASESEXERCISE - Section-B
13 Videos
Similar Questions
Knowledge Check
The initial velocity of a body moving along a straight lines is 7m/s. It has a uniform acceleration of 4m/s2 the distance covered by the body in the 5th second of its motion is-
A25mB35mC50mD85mThe velocity function of an object moving along a straight line is given by v(t)=At2+Bt. If at t=2s, the velocity is 3 m/s and acceleration is 0.500m/s2, find the value of the constant A.
A−0.5m/s3B−0.5m/s2C−2.5m/s3D−1.5m/s2The position of a particle moving in a straight line is given by
x=3t3−18t2+36t
Here, x is in m and t in second. ThenAdirection of velocity and acceleration both change at t=2sBthe distance travelled by particle is equal to magnitude of displacement for t=0 to t=5sCthe speed of particle is decreasing in t=0 to t=2s then it is increasing for t>2DThe magnitudes of velocity and acceleration are equal at t=0
Velocity (in m/s) of a particle moving in a straight line given by v=(t2−2t1). Match Table-1 with Table -2
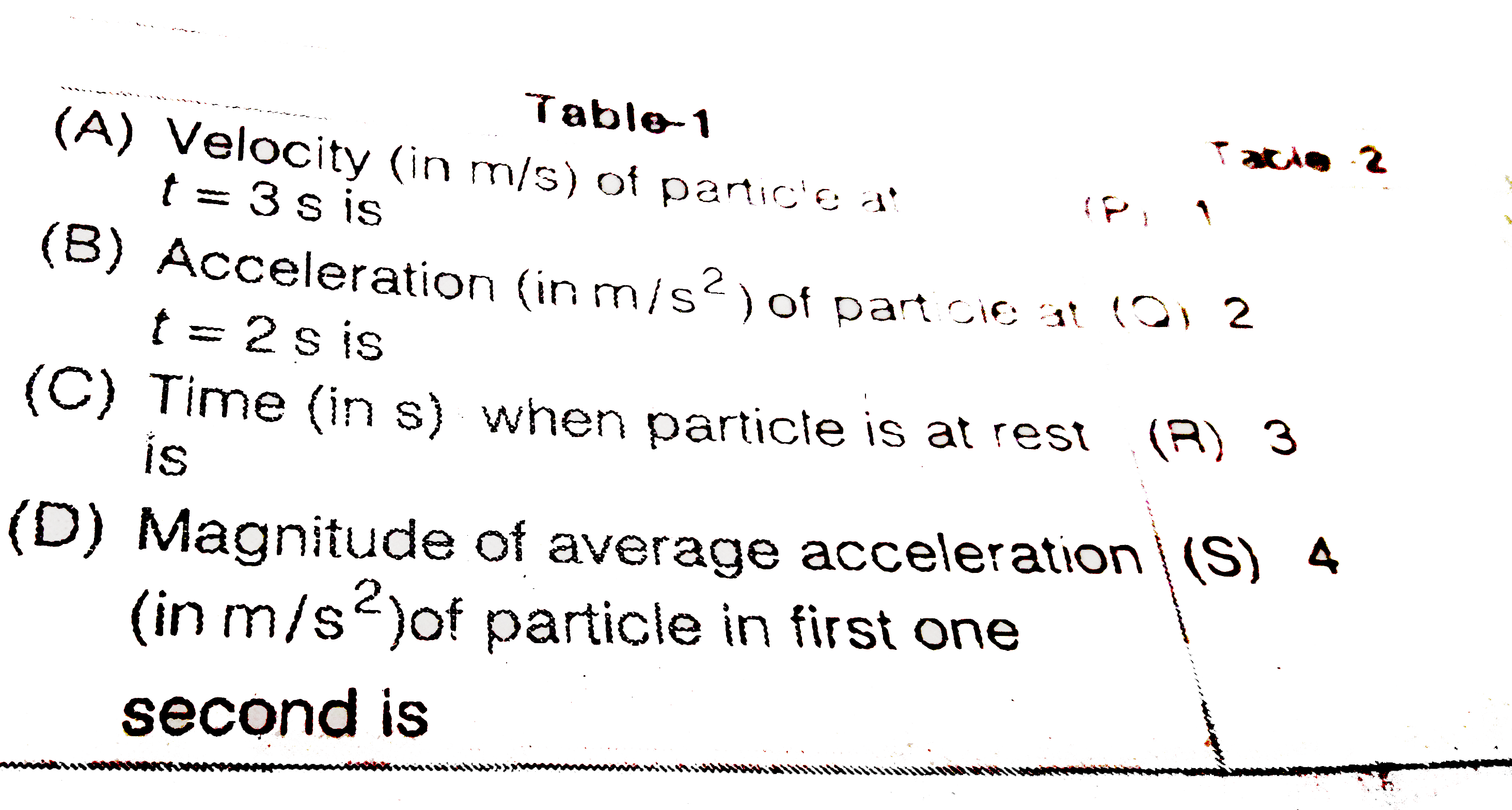
View SolutionIf the velocity of a body related to displacement x is given by v=√5000+24x m/s, then the acceleration of the body is _______m/s2.
View SolutionThe velocity v of a body moving along a straight line varies with time t as v=2t2e−t, where v is in m/s and t is in second. The acceleration of body is zero at t =
View SolutionVelocity of particle moving along x-axis is given as v=(x3−x2+2) m/sec. Find the acceleration of particle at x=2 meter.
View SolutionIf the velocity of a particle is given by v=(180−16x)12ms, then its acceleration will be
View Solution
