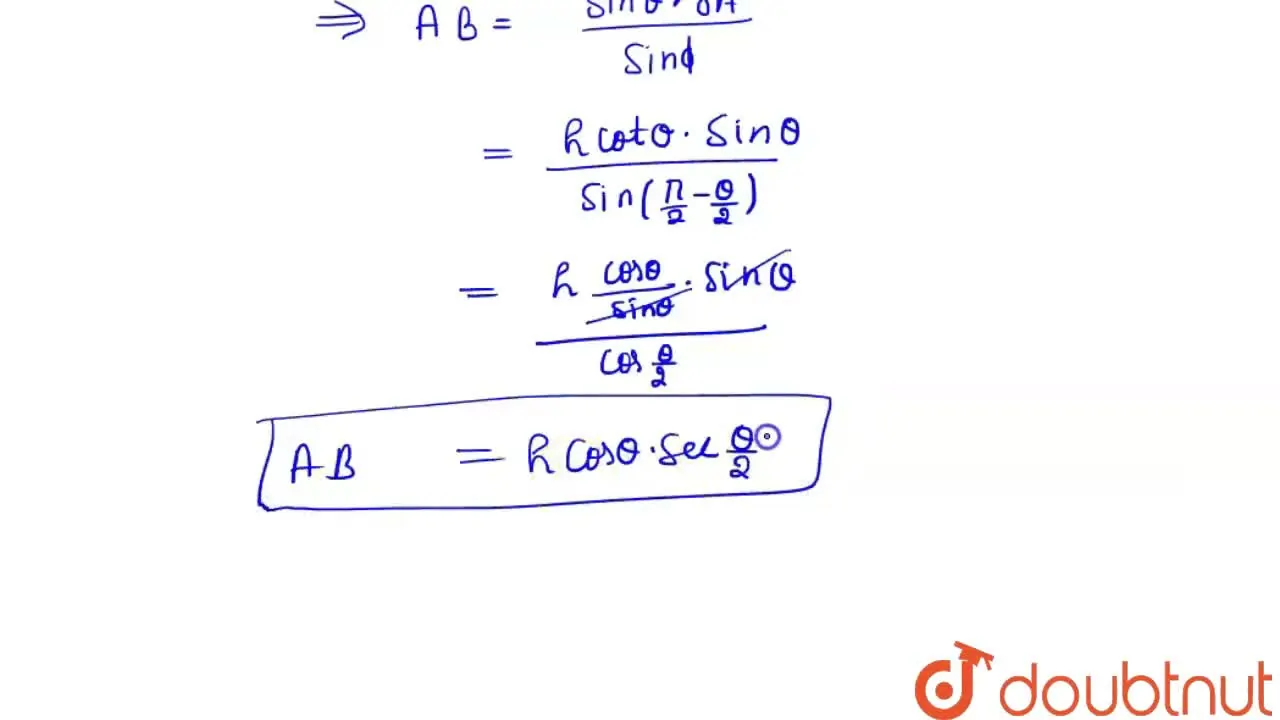
A and B are two points in the horizontal plane through O,, the foot of a pillar OP of height h such that ∠AOB=θ. If the elevation of the top of the pillar from A and B are also equal to θ, then AB is equal to
hcotθ
hcosθsecθ2
hcotθ sinθ2
hcosθcosecθ2
The correct Answer is:B
Step by step video, text & image solution for A and B are two points in the horizontal plane through O,, the foot of a pillar OP of height h such that angleAOB=theta. If the elevation of the top of the pillar from A and B are also equal to theta, then AB is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ML KHANNACHAPTER - HEIGHTS AND DISTANCESEXERCISE - Problem Set (1) TRUE AND FALSE11videos
HEIGHTS AND DISTANCES
- BOOK - ML KHANNACHAPTER - HEIGHTS AND DISTANCESEXERCISE - Problem Set (1) FILL IN THE BLANKS21videos
HEIGHTS AND DISTANCES
- BOOK - ML KHANNACHAPTER - FUNCTIONSEXERCISE - SELF ASSESSMENT TEST10videos
FUNCTIONS
- BOOK - ML KHANNACHAPTER - INEQUALITIESEXERCISE - PROBLEM SET (1)(FILL IN THE BLANKS)4videos
INEQUALITIES
Similar Questions
A and B are two points in the horizontal plane through O, the foot of pillar OP of height h such that ∠AOB=θ. If the elevation of the top of the pillar from A and B are also equal to θ, then AB is equal to
View SolutionFrom two points on the ground and lying on a straight line through the foot of a pillar, the two angles of elevation of the top of the pillar are complementary to each other. If the distances of the two points from the foot of the pillar are 12 metres and 27 metres and the two points lie on the same side of the pillar, then the height (in metres) of the pillar is:
View SolutionFrom two points on the ground lying on a straight line through the foot of a pillaer , the two angles of elevation of the top of the pillar are complementary to each other . If the distance of the two points from the foot of the pillar are 9 metres and 16 metres and the two points lie on the same side of the pillar , then the height of the pillar is
View SolutionA, B, C are three points on a horizontal line through the base O of a pillar OP, such that OA, OB, OC are in A.P. If α,β,γ the angles of elevation of the top of the pillar at A, B, C respectively are also in A.P. then sinα,sinβ,sinγ are in
View SolutionThe angles of depression of two points A and B on a horizontal plane such that AB= 200 from the top P of a tower PQ of height 100 are 45−θ and 45+θ. If the line AB Passes through Q the foot of the tower, then angle θ is equal to
View SolutionThe angle of elevation of the top Q of a tower PQ at a point A on the horizontal plane through P the foot of the tower is α. At a point B on AQ at a vertical height of a, the angle of elevation of the middle point R of the tower PQ is β, then the height of the tower is
View SolutionThe angles of depression of two points A and B on a horizontal plane such that AB= 200 from the top P of a tower PQ of height 100 are 45−θ and 45+θ. If the line AB Passes through Q the foot of the tower, then angle θ is equal to
View SolutionPQ is a vertical tower having P as the foot. A,B,C are three points in the horizontal plane through P. The angles of elevation of Q from A,B,C are equal and each is equal to θ . The sides of the triangle ABC are a,b,c, and area of the triangle ABC is . Then prove that the height of the tower is (abc) tanθ4.
View SolutionABCD is a square plot . The angle of elevation of the top of a pole standing at D from A and C is 30∘ and that from B is θ, then tanθ is equal to
View SolutionABCD is a square, Plot. The angle of elevation of the top of a pole standing at D from A or C is 30∘ and that from B is θ, then tanθ is equal to
View Solution