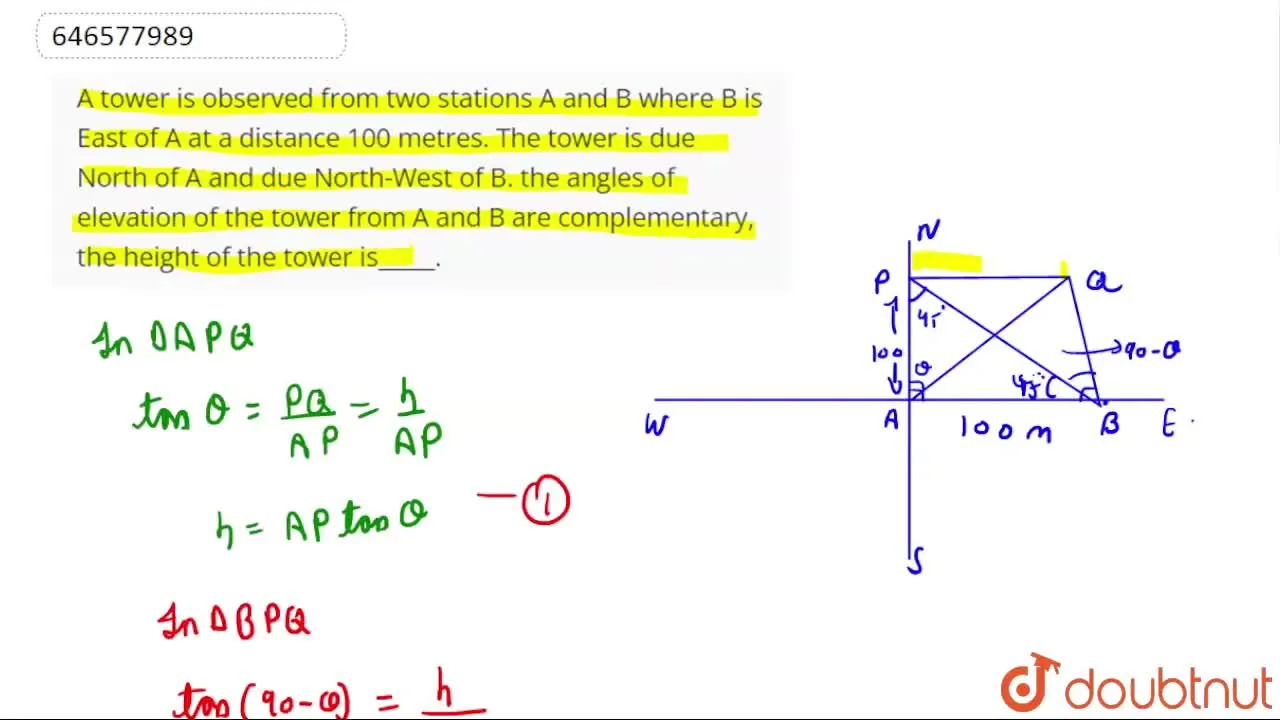
A tower is observed from two stations A and B where B is East of A at a distance 100 metres. The tower is due North of A and due North-West of B. the angles of elevation of the tower from A and B are complementary, the height of the tower is_____.
The correct Answer is:100(2)1/4
Step by step video, text & image solution for A tower is observed from two stations A and B where B is East of A at a distance 100 metres. The tower is due North of A and due North-West of B. the angles of elevation of the tower from A and B are complementary, the height of the tower is_____. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - ML KHANNACHAPTER - HEIGHTS AND DISTANCESEXERCISE - Problem Set (3) TRUE AND FALSE11videos
HEIGHTS AND DISTANCES
- BOOK - ML KHANNACHAPTER - FUNCTIONSEXERCISE - SELF ASSESSMENT TEST10videos
FUNCTIONS
- BOOK - ML KHANNACHAPTER - INEQUALITIESEXERCISE - PROBLEM SET (1)(FILL IN THE BLANKS)4videos
INEQUALITIES
Similar Questions
The angle of elevation of a tower from a distance 100 m from its foot is 30∘ .Height of the tower is :
View SolutionThe angle of elevation from two points at a distance of x and y from the feet of a Tower are complementary, the height of the Tower is
View SolutionPQ is a part of a given height a and AB is a tower at some distance, αandβ are the angles of elevation of B, the top of the tower at P and Q respectively. The height of the tower is
View SolutionFrom a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ . The height of the tower is
View SolutionIf the distance of a point from the tower is equal to the height of the tower , then find the angle of elevation of the top of the tower from that point .
View SolutionThe angle of elevation of the top of a tower from a point 20 metres away from its base is 45∘. The height of the tower is
View SolutionThe angle of elevation of the top of a tower from two distinct points s and t from foot are complementary. Prove that the height of the tower is √st.
View SolutionFrom 40 m away from the foot of a tower , the angle of elevation of the top of the tower is 60∘ .What is the height of the tower ?
View SolutionTwo houses are collinear with the base of a tower and are at distance 3 m and 12 m (on the same side) from the base of the tower. The angles of elevation from these two houses of the top of the tower are complementary. What is the height of the tower ?
View SolutionThe angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is √st.
View Solution