Question

A two- dimensional solid is made by alternating circles with radius a and b such that the sides of the circles touch. The packing fraction is defined as the ratio of the are under the circles to the area under the rectangle with sides of the length x and y.

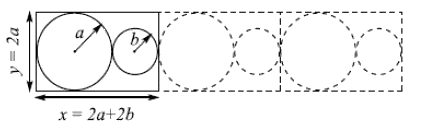
The ratio r = b/a for which the packing fraction is minimized is closed to :

Options

A. `0.41`
B. `1.0`
C. `0.50`
D. `0.32`

Answer

A

Explanation

Area of rectangle ` =xy`
`= 2a (2a +2b)`
`= 4a (a+b)`
Area covered by circles `= pi a^2 + pi b^2 = pi ( a^2 +b^2)`
Packing fraction `(P.F) = ( pi (a^2 +b^2))/( 4 (a^2 + ab))`
` = ( pi a^2 (1 + (b^2))/(a^2))/(4a^2 (1+ (b)/(a)))`
putting ` r= (b/a)`
` P.F = ( pi ( 1+ r^2))/( 4 (1 +r))`
for minimum P.F ` (d (P.F))/( d r) =0`
` or (pi)/(4) [ ( 2 r (1+r) -(1-r^2))/((1+r)^2)]=0`
` or r = (-2 + sqrt(4 +4))/(2) = sqrt(2) -1=0.414`
Answer is option (A)