The area of a square is equal to the area of a circle. What is the ratio between the side of the square and the radius of the circle?
√π:1
1:√3
1:π
π:1
The correct Answer is:A
To solve the problem step by step, we need to find the ratio between the side of a square and the radius of a circle, given that their areas are equal.
Step 1: Write the formulas for the areas
The area of a square (A_square) is given by:
Asquare=S2
where S is the side length of the square.
The area of a circle (A_circle) is given by:
Acircle=πR2
where R is the radius of the circle.
Step 2: Set the areas equal to each other
Since the problem states that the area of the square is equal to the area of the circle, we can write:
S2=πR2
Step 3: Rearrange the equation to find the ratio
To find the ratio SR, we can rearrange the equation:
S2R2=π
Taking the square root of both sides gives:
SR=√π
Step 4: Write the ratio in the required form
Thus, the ratio of the side of the square to the radius of the circle can be expressed as:
S:R=√π:1
Final Answer
The ratio between the side of the square and the radius of the circle is:
S:R=√π:1
---
The area of a square (A_square) is given by:
Asquare=S2
where S is the side length of the square.
Acircle=πR2
where R is the radius of the circle.
Since the problem states that the area of the square is equal to the area of the circle, we can write:
S2=πR2
To find the ratio SR, we can rearrange the equation:
S2R2=π
SR=√π
Thus, the ratio of the side of the square to the radius of the circle can be expressed as:
S:R=√π:1
The ratio between the side of the square and the radius of the circle is:
S:R=√π:1
Topper's Solved these Questions
- MENSURATIONBook:RS AGGARWALChapter:MENSURATIONExercise:TEST PAPER
Explore 10 Videos
- MENSURATIONBook:RS AGGARWALChapter:MENSURATIONExercise:TEST PAPER (M.C.Q)
Explore 9 Videos
- MENSURATIONBook:RS AGGARWALChapter:MENSURATIONExercise:EXERCISE 20F
Explore 16 Videos
- LINES AND ANGLESBook:RS AGGARWALChapter:LINES AND ANGLESExercise:Exercise 13
Explore 11 Videos
- PERCENTAGE Book:RS AGGARWALChapter:PERCENTAGE Exercise:TEST PAPER
Explore 16 Videos
Similar Questions
Knowledge Check
The area of a square is 16π of the area of a circle. The ratio of the sides of the square to the diameter of the circle is
A3:1B2:1Cπ:1D√2π:1The areas of a circle and a square are same. The ratio of the side of the square to the radius of the circle is
A2π:1B1:√πC√π:1D1:πThe area of square is 16π of the area of circle . The ratio of the side of the square to the diameter of the circle is
A3:1B2:1Cπ:1D√2π:1
The areas of a circle and a square are same. The ratio of the side of the square to the radius of the circle is
View SolutionThe area of square is 16π area of a circle. The ratio of the side of the square to the diameter of the circle is
View SolutionThe area of a circle is same as the areas of a square. What is the ratio of the diameter of the circle and diagonal of the square ?
View SolutionIn the adjoining diagram ABCD is a square with side 'a' cm. In the diagram the area of the larger circle with centre 'O' is equal to the sum of the areas of all the rest four circles with equal radii, whose centres are P,Q,R and S . What is the ratio between the side of square and radius of a smaller circle ?
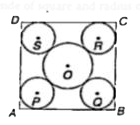
View SolutionThe area of a circle is same as the areas of a square. What is the ratio of the diameter of the circle and diagonal of the square ?
View Solution