Consider a reaction that is first order in both direction
$A \overset{k_{f}}{\underset{k_{b}}{\Leftrightarrow}} B$
Initially only A is present , and its concentration is $A_{0}$ . Assume $A_{t}$ and $A_{e q}$ are the concentrations of A at time 't' and at equilibrium, respectively. The time 't at which $A_{t} = (A_{0} + A_{e q}) / 2 i s$ ,

A

$t = \frac{I n (\frac{3}{2})}{(K_{f} + k_{b})}$

B

$t = (I n) \frac{(\frac{3}{2})}{(k_{f} - k_{b})}$

C

$t = \frac{I n 2}{(k_{f} + K_{b})}$

D

$t = \frac{I n 2}{(K_{f} - K_{b})}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

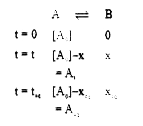
Given at time $t = t A_{t} = \frac{A_{0} + A_{e q}}{2}$
and $x_{e q} = A_{0} - A_{e q}$
Now $t = \frac{1}{k_{f} + k_{b}} \ln (\frac{x_{c}}{x_{e - x}}) = (\frac{l n 2}{k_{f} + k_{b}})$

|

Updated on:21/07/2023

Class 12 CHEMISTRY QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
For the reaction $A K_{1} \Leftarrow === \Rightarrow K_{2} B$ , if 'a' is the initial concentration of A and n is the number of moles of A reacting if initially no B was present then :
A $\frac{d x}{d t} = [K_{1} (a - x) - K_{2} x]$ initially
B $K_{1} (a - x_{e}) - K_{2} x_{e} = 0$ at equilibrium
C $K_{1} + K_{2} = K_{1} . \frac{a}{x e}$
D $(K_{1} + K_{2}) = \frac{1}{t} ln . \frac{x_{e}}{x_{e} - x}$
Question 2 - Select One
If [A] is the concentration of A at any time t and ${[A]}_{0}$ is the concentration at t=0 , then for the $1^{s t}$ order reaction , the rate equation can be written as _____.
A $k = \frac{2.303}{t} {log}_{10}$ $\frac{{[A]}_{t}}{{[A]}_{0}}$
B $k t = 2.303 {log}_{10}$ $\frac{{[A]}_{0}}{{[A]}_{t}}$
C $k = \frac{2.303}{t} {log}_{10}$ $\frac{{[A]}_{0}}{{[A]}_{0} - {[A]}_{t}}$
D $k = \frac{2.303}{t} {log}_{10}$ $\frac{{[A]}_{0} - {[A]}_{t}}{{[A]}_{0}}$
Question 3 - Select One
For a first order reaction : $A \to n B$ (with $n$ -possibly fractional), the concentration of the product varies with time as ( $A_{0}$ is the concentration of A at time $t = 0$ ).
A $[B] = n A_{0} (1 - e^{- 2 k t})$
B $[B] = n A_{0} t$
C $[B] = n A_{0} (1 - e^{- k t})$
D $[B] = n A_{0} (e^{- k t})$

KVPY PREVIOUS YEAR-QUESTION PAPER 2020-PART-II(CHEMISTRY)

Home
Ask Doubt
Profile