An initially uncharged capacitor C is being charged by a battery of emf E through a resistance R upto the instant when the capacitor is charged to the potential E/2, the ratio of the work done by the battery to the heat dissipated by the resistor is given by :-
2:1
3:1
4:3
4:1
The correct Answer is:C
To solve the problem, we need to find the ratio of the work done by the battery to the heat dissipated by the resistor when a capacitor is charged to a potential of E2.
1. Understand the Charging of the Capacitor:
The capacitor C is charged by a battery of emf E through a resistor R. The voltage across the capacitor when charged is V=E2.
2. Calculate Charge on the Capacitor:
The charge Q on the capacitor when it is charged to E2 is given by:
Q=C⋅V=C⋅E2=CE2
3. Determine the Total Charge:
The maximum charge Q0 that the capacitor can hold when fully charged to E is:
Q0=C⋅E
4. Use the Charging Equation:
The charge Q at time t during charging is given by:
Q=Q0(1−e−tRC)
Setting Q=CE2 and Q0=CE, we have:
CE2=CE(1−e−tRC)
Simplifying gives:
12=1−e−tRC
Rearranging leads to:
e−tRC=12
Taking the natural logarithm:
−tRC=ln(12)⟹t=−RCln(12)=RCln(2)
5. Calculate Work Done by the Battery:
The work done W by the battery in charging the capacitor is given by:
W=Q⋅V=(CE2)⋅E=CE22
6. Calculate Heat Dissipated by the Resistor:
The heat H dissipated in the resistor can be calculated using the formula:
H=∫t0I2Rdt
The current I can be expressed as:
I=dQdt=CERe−tRC
Therefore,
H=∫RCln(2)0(CERe−tRC)2Rdt
Simplifying this integral leads to:
H=C2E2R∫RCln(2)0e−2tRCdt
Evaluating the integral yields:
H=C2E2R(−RC2e−2tRC)RCln(2)0=C2E2R⋅RC2(1−14)=3CE28
7. Calculate the Ratio:
Finally, the ratio of work done by the battery to the heat dissipated is:
Ratio=WH=CE223CE28=43
Final Answer:
The ratio of the work done by the battery to the heat dissipated by the resistor is 43.
The capacitor C is charged by a battery of emf E through a resistor R. The voltage across the capacitor when charged is V=E2.
The charge Q on the capacitor when it is charged to E2 is given by:
Q=C⋅V=C⋅E2=CE2
The maximum charge Q0 that the capacitor can hold when fully charged to E is:
Q0=C⋅E
The charge Q at time t during charging is given by:
Q=Q0(1−e−tRC)
Setting Q=CE2 and Q0=CE, we have:
CE2=CE(1−e−tRC)
Simplifying gives:
12=1−e−tRC
Rearranging leads to:
e−tRC=12
Taking the natural logarithm:
−tRC=ln(12)⟹t=−RCln(12)=RCln(2)
The work done W by the battery in charging the capacitor is given by:
W=Q⋅V=(CE2)⋅E=CE22
The heat H dissipated in the resistor can be calculated using the formula:
H=∫t0I2Rdt
The current I can be expressed as:
I=dQdt=CERe−tRC
Therefore,
H=∫RCln(2)0(CERe−tRC)2Rdt
Simplifying this integral leads to:
H=C2E2R∫RCln(2)0e−2tRCdt
Evaluating the integral yields:
H=C2E2R(−RC2e−2tRC)RCln(2)0=C2E2R⋅RC2(1−14)=3CE28
Finally, the ratio of work done by the battery to the heat dissipated is:
Ratio=WH=CE223CE28=43
The ratio of the work done by the battery to the heat dissipated by the resistor is 43.
Topper's Solved these Questions
Similar Questions
An Uncharged capacitor C is connected to a battery through a resistance R. Show that by the time the capacitor gets fully charged, the energy dissipated in R is the same as the energy stored in C.
View SolutionA capacitor is getting charged by a battery of emf V what is the ratio of heat dissipated in the resistor to work done by battery when charge on capacitor is CV/2
View Solution
Knowledge Check
An uncharged capacitor is fully charged with a battery . The ratio of energy stored in the capacitor to the work done by the battery in this process is
A1:2B2:1C1:1D2:3When a charged capacitor is discharged through a resistor, heat is produced in the resistor
In charging a capacitor, energy is stored in the capacitor.ABoth A and R falseBBoth A and R true and R is not correct reason for ACA is true and R is falseDBoth A and R are true and R is correct reason of A.If initial charge on all the capacitors were zero , work done by the battery in the circuit shown is
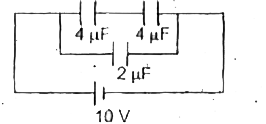 A0.2 mJB200 mJC0.4 mJD400 mJ
A0.2 mJB200 mJC0.4 mJD400 mJ
A capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionFour uncharged capacitors are charged by 24V battery as shown in the figure. How much charge flows through switch S when it is closed?
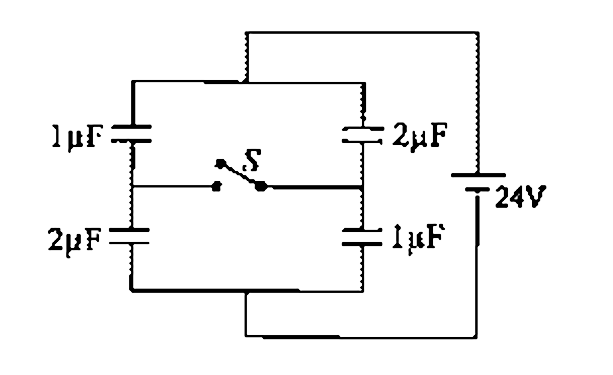
View SolutionThe plates of a parallel plate capacitor are charged with a battery so that the plates of the capacitor have acquired the P.D. equal to e.m.f of the battery. The ratio of the work done by the battery and the energy stored in capacitor is
View SolutionIf and uncharged capacitor is charged by connected it to a battery, then the amount of energy lost as heat is.
View SolutionA capacitor of capacitance C is charge by a battery of emf E and internal resistance r. A resistasnce 2 is also connet in sereis with the capacitor. The amount of heat liberated inside the battery by the time capacitor is 50% charged is
View Solution

