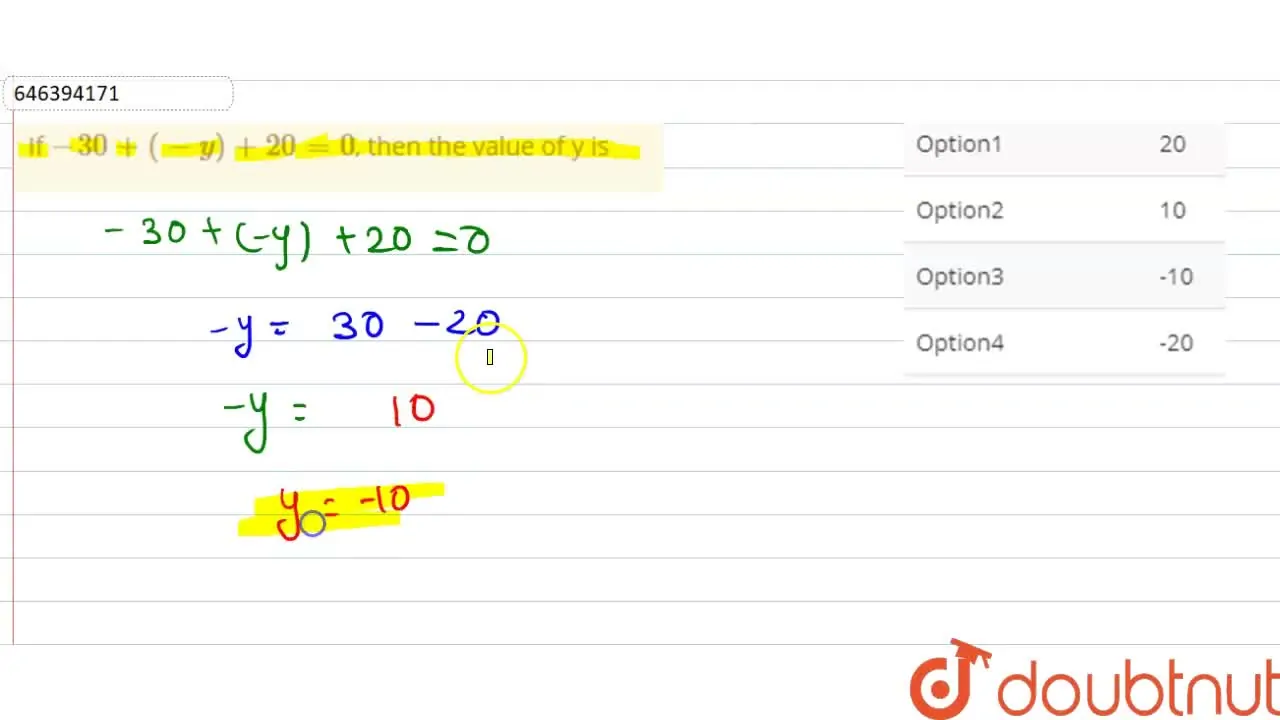
If −30+(−y)+20=0, then the value of y is
20
10
-10
-20
Step by step video & image solution for If -30+(-y)+20=0, then the value of y is by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Related Playlists
Similar Questions
If sin(3x−20∘)=cos(3y+20∘), then the value of (x + y) is
View SolutionIf x(x+y+z)=20,y(x+y+z)=30andz(x+y+z)=50 the vaue of 2 (x + y + z) is
View SolutionIf x(x+y+z)=20,y(x+y+z)=30andz(x+y+z)=50 the vaue of 2 (x + y + z) is
View SolutionIf x , y are acute angles , 0<x+y<90∘andsin(2x−20∘)=cos(2y+20∘) , then the value of tan (x+y) is :
View SolutionIf the straight line y=mx lies outside the circle x2+y2−20y+90=0, then the value of m will satisfy
View SolutionA parabola with vertex (2, 0) and axis of symmetry parallel to the y-axis, passes through (3, 1) and (−3,t), then the value of t is. 30 (b) 35 (c) 20 (d) 25
View SolutionIf x + y = 52 and x - y = 20, then find the value of x : y.
यदि x + y = 52 तथा x - y = 20 है, तो x : y का मान कितना है?View SolutionLet x=(logsin300cos300)(logcos30∘cot300)(logcot300cosec300) and y=3logcot300(|x|+3) then the value of y is
View SolutionIf tanx+tany=25 and cotx+coty=30 then the value of tan(x+y) is
View SolutionIf x2+y2+siny=4, then the value of d2ydx2 at the point (−2,0) is
View Solution