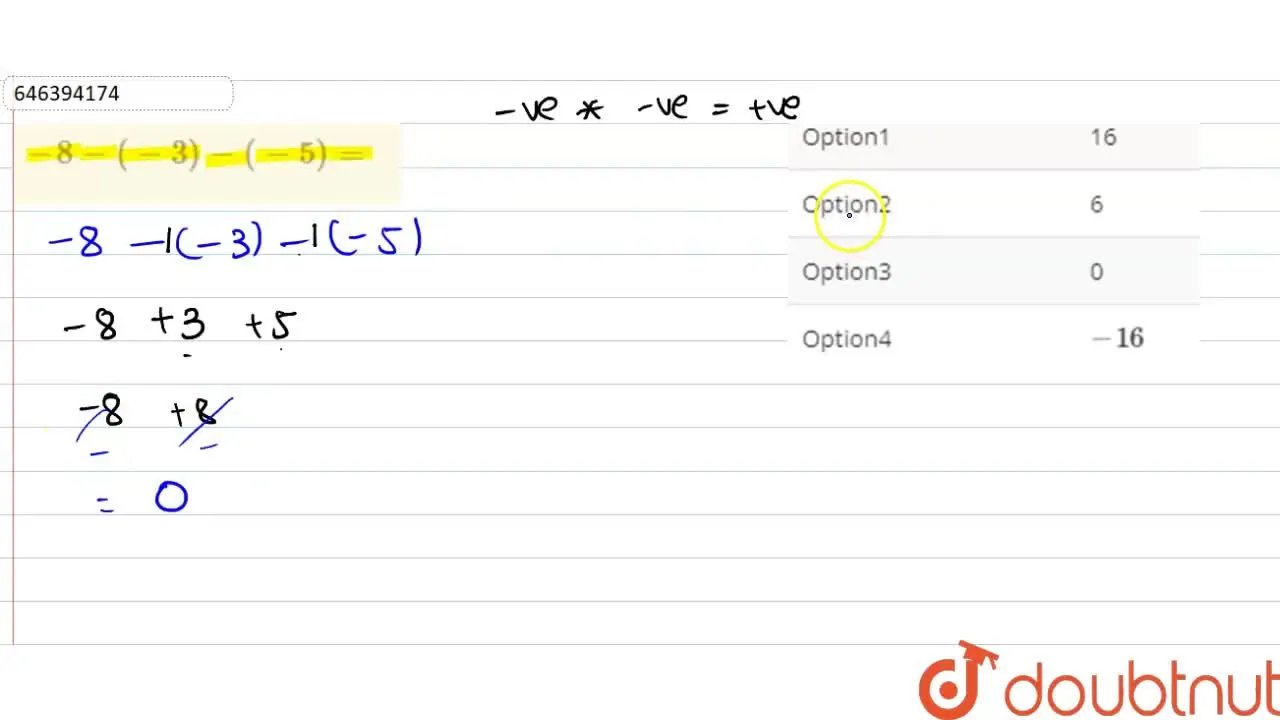
−8−(−3)−(−5)=
A
16
B
6
C
0
D
−16
Video Solution
|
Answer
Step by step video & image solution for -8-(-3)-(-5)= by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Updated on:21/07/2023
Related Playlists
Similar Questions
Verify that x=8 is a solution of the equation 5x−48−x−35=x+64
View SolutionEvaluate: 8−[5−(−3+2)]÷2|5−3|−|5−8|÷3 (a) 2 (b) 3 (c) 4 (d) 5
View Solution[(−13)8÷(−13)5]−[(−13)5÷(−13)3]
View Solution56÷7⋅838+5
View SolutionIf A=[31−12] then A2= (A) [8−5−53] (B) [8−553] (C) [8−5−5−3] (D) [85−53]
View SolutionEvaluate : 8−[5−(−3+2)]+2|5−3|−|5−8|+3
View SolutionSimplify: (139×−152)+ (73×85)+(35×12)
View SolutionProve that: sin(3pi8−5)cos(pi8+5)+cos(3pi8−5)sin(pi8+7)=1
View SolutionSimplify: 38+72+ −35+98+ −32+65
View SolutionSimplify: 38+72+ −35+98+ −32+65
View Solution