if a,b,c,d,e and f are six real numbers such that a+b+c=d+e+f a2+b2+c2=d2+e2+f2 and a3+b3+c3=d3+e3+f3 , prove by mathematical induction that an+bn+cn=dn+en+fn∀n∈N. Solution in Punjabi
Let P(n):an+b2+cn=dn+en+fn,∀n∈N ..(i)
where a+b+c+d=e+ ...(ii)
a2+b2+c=d2+e2+f ....(iii)
and a2+b3+c3=d3+e2+3 ...(iv)
Step I from n from Eq. (i) we get
P(1):a+b+c=d+e+f [ given]
Hence the result is true for n 1
Also, for n=2 from Eq(i), we get
P(2):a2+b2+c2=d2+e3+f3 [ given]
Hennce the result true or n=3
Therefore, P(1) , P(2) and P (3) are true.
Step II Assume that P(k−2),P(k−1)andP(k) are true, then
P(k−2),ak−2+bk−2=dk−2+ek−2+f)k−2) ...(v)
p(k−1):a−1+bk−1+ck−1=dk−1+ek−1+fk−1 ....(vi)
and P(k):ak+bk+ck=dk+ek+fk m ...(vii)
Step III for xn=k+1 we shall to prove that
P(k+1):ak+1+bk+1=dk+1+ek+1+fk+1
LHS =ak+1+bk+1+ck+1
=(ak+bk(a+b+c)−(ak−1+bk−1+ck−1)
(ab+bc+ca)+abc(ak−2+bk−2+bk−2+ck−2)
=(dk+ef+fk)(d+e+f)−(dk−1+ek−1+ck−2)
(de+ef+fd)+def(dk−2+ek−2+fk−2)
[ using Eqs. (ii), (iii), (iv), (v), (vi), (vii)]
∴(a+b+c)2=(d+e+f)2
⇒a2+b2+c2+2(ab+bc+ca)
=d2+e2+f2+2(de+ef+fd)
⇒ab+bc+ca=de+ef+fd
[∴a2+b2+c2=d2+e2+f2]
and a3+b3+c3−3abc
(=d+e+f)(d2+e2+f2−de−ef−fd)
=d3+e3+f3−edf
⇒abc=def[∴a3+b3+c3=d3+e3+f3)
=dk+1+ek+1+fk−1=RHS
This shows that result is true for n=k+1. Hence by second perincipal of mathmatical inducition, the result is true for all n∈N.
Topper's Solved these Questions
- MATHEMATICAL INDUCTION BOOK - ARIHANT MATHSCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
- MATHEMATICAL INDUCTION BOOK - ARIHANT MATHSCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise (Statement I And Ii Type Questions)
3 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
4 Videos
- MATRICES BOOK - ARIHANT MATHSCHAPTER - MATRICES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
49 Videos
Similar Questions
If t₁+t₅+t15+t₁₀+t₂₀+t₂₄=225 Find the sum of first 24th term of that A.P?
View SolutionIf a1=1,a2=5 find the common difference and 5th term of A.P
View SolutionIn Which quadrant Point (−2,−3) will be lie.
View SolutionLet A=⎡⎢⎣1000110−24⎤⎥⎦,I=⎡⎢⎣100010001⎤⎥⎦andA−1=[16(A2+cA+dI)] Then value of candd are (a) (−6,−11) (b) (6,11) (c) (−6,11) (d) (6,−11)
View SolutionLet f, g and h be real-valued functions defined on the interval [0, 1] by f(x)=ex^2+e−x^2, g(x)=xex^2+e−x^2 and h(x)=x2ex^2+e−x^2 . If a,b, and c denote respectively, the absolute maximum of f, g and h on [0, 1], then a=b and c≠b (b) a=c and a≠b a≠b and c≠b (d) a=b=c
View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of ABC. Then DEF is congruent to triangle. ABC (b) AEF (c) BFD, CDE (d) AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
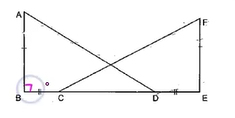
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that: ar(EFC)=12ar(EBF)
View SolutionLet A and B be two sets such that n(A)=5 and n(B)=2, if a, b, c, d, e are distinct and (a,2), (b,3), (c,2), (d,3), (e,2) are in A×B , find A and B.
View SolutionLet M=⎡⎢⎣abcdef111⎤⎥⎦andN=M22. If (a−b)2+(d−e)2=36,
(b−c)2+(e−f)2=64,
(a−c)2+(d−f)2=100, then value of |N| is equal to
View Solution(n(A ∪ B ∪ C))=n(A)+n(B)+n(C)-n(A ∩ B)-n(B ∩ C)-n(A ∩ C)+n(A ∩B∩ C) என்பதைக் கீழ்க்காணும் கணங்களுக்குச் சரிபார்க்க ? A{a,c,e,f,h},B={c,d,e,f}மற்றும் C={a,b,c,f}
View SolutionIf a:b=c:d=e:f then (pa+qc+re):(pb+qd+rf) is equal to
View SolutionIf n∑r=1r(r+1)(2r+3)=an4+bn3+cn2+dn+e, then (a) a−b=d−c (b) e=0 (c) a,b−2/3,c−1 are in A.P. (d) (b+d)/a is an integer
View SolutionIn Figure, it is given that AB=EF, BC=DE, AB ⊥BD and FE ⊥CE. Prove that ABD ≅FEC.
View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of △ABC. Then DEF is congruent to triangle.
(a)ABC
(b) AEF
(c) BFD, CDE
(d) AFE, BFD, CDE
View SolutionIn Figure, AB⊥BE and FE ⊥BE. If BC=DE and AB=EF, then ABD is congruent to: EFC (b) ECF (c) CEF (d) FEC
View Solution
