In parallel combination, the effective resistance (of R1 and R2) is given by
R=R1R2R1+R2
1R=1R1+1R2
R=R1+R2
R=1R1+1R2
The correct Answer is:A, B, D
To find the effective resistance of two resistors R1 and R2 connected in parallel, we can use the formula for the effective resistance Reff in a parallel circuit.
1. Understand the Parallel Connection: In a parallel connection, the voltage across each resistor is the same, but the current through each resistor can be different.
2. Use the Formula for Effective Resistance: The formula for the effective resistance Reff of two resistors R1 and R2 in parallel is given by:
1Reff=1R1+1R2
3. Rearranging the Formula: To find Reff, we can rearrange the formula:
Reff=1(1R1+1R2)
4. Finding a Common Denominator: To simplify the right-hand side, we can find a common denominator:
1Reff=R2+R1R1R2
5. Final Expression for Effective Resistance: Therefore, the effective resistance Reff can be expressed as:
Reff=R1R2R1+R2
Final Answer:
The effective resistance Reff of resistors R1 and R2 in parallel is given by:
Reff=R1R2R1+R2
1Reff=1R1+1R2
Reff=1(1R1+1R2)
1Reff=R2+R1R1R2
Reff=R1R2R1+R2
The effective resistance Reff of resistors R1 and R2 in parallel is given by:
Reff=R1R2R1+R2
Topper's Solved these Questions
- SOURCES OF ELECTRIC CURRENTBook:CENGAGE PHYSICSChapter:SOURCES OF ELECTRIC CURRENTExercise:MANDATORY EXERCISE (Exercise Set III)
Explore 1 Video
- SOURCES OF ELECTRIC CURRENTBook:CENGAGE PHYSICSChapter:SOURCES OF ELECTRIC CURRENTExercise:MANDATORY EXERCISE (Exercise Set IV)
Explore 9 Videos
- SOURCES OF ELECTRIC CURRENTBook:CENGAGE PHYSICSChapter:SOURCES OF ELECTRIC CURRENTExercise:MANDATORY EXERCISE (Exercise Set I)
Explore 4 Videos
- REFRACTION OF LIGHT Book:CENGAGE PHYSICSChapter:REFRACTION OF LIGHT Exercise:OLYMPIAD AND NSE LEVEL EXCERCISES
Explore 10 Videos
- STATIC ELECTRICITYBook:CENGAGE PHYSICSChapter:STATIC ELECTRICITYExercise:OLYMPIAD AND NTSE LEVEL EXERCISES
Explore 10 Videos
Similar Questions
When resistres of resistyences R1R2andR3 are connected in series , then the resistanceR1 is given by R1=R1+R2+R3
In this arrengement the current through each resister is same hut potential difference across then is difference
When resitorce of resistance R1R2andR3 are connected in particle the effective resistance Rp is given by 1Rp=1R1+1R2+1R3
In this arrangement , the potential difference across each resistance is but current through then is difference
Read the above passage and answer the following question :
(i) Why does the effective resistance increase in series ?
(ii) Why does the effective resistance decrease in parallel ?
(iii) What basic value are displayed by the above study ?
View Solution(a) what is meant by series and parallel combination of resistances ?
(b) in which case, series combination or parallel combination, the combined resistance is less than any of the individual resistances ?
(c ) How should two resistance of 2Ω each be connected so as to produce an equivalent resistance of 1Ω ?
In the circuit diagram given here , find:
(i) total resistance of the circuit
(ii) total current flowing in the circuit, and
(iii) the potential difference across R1
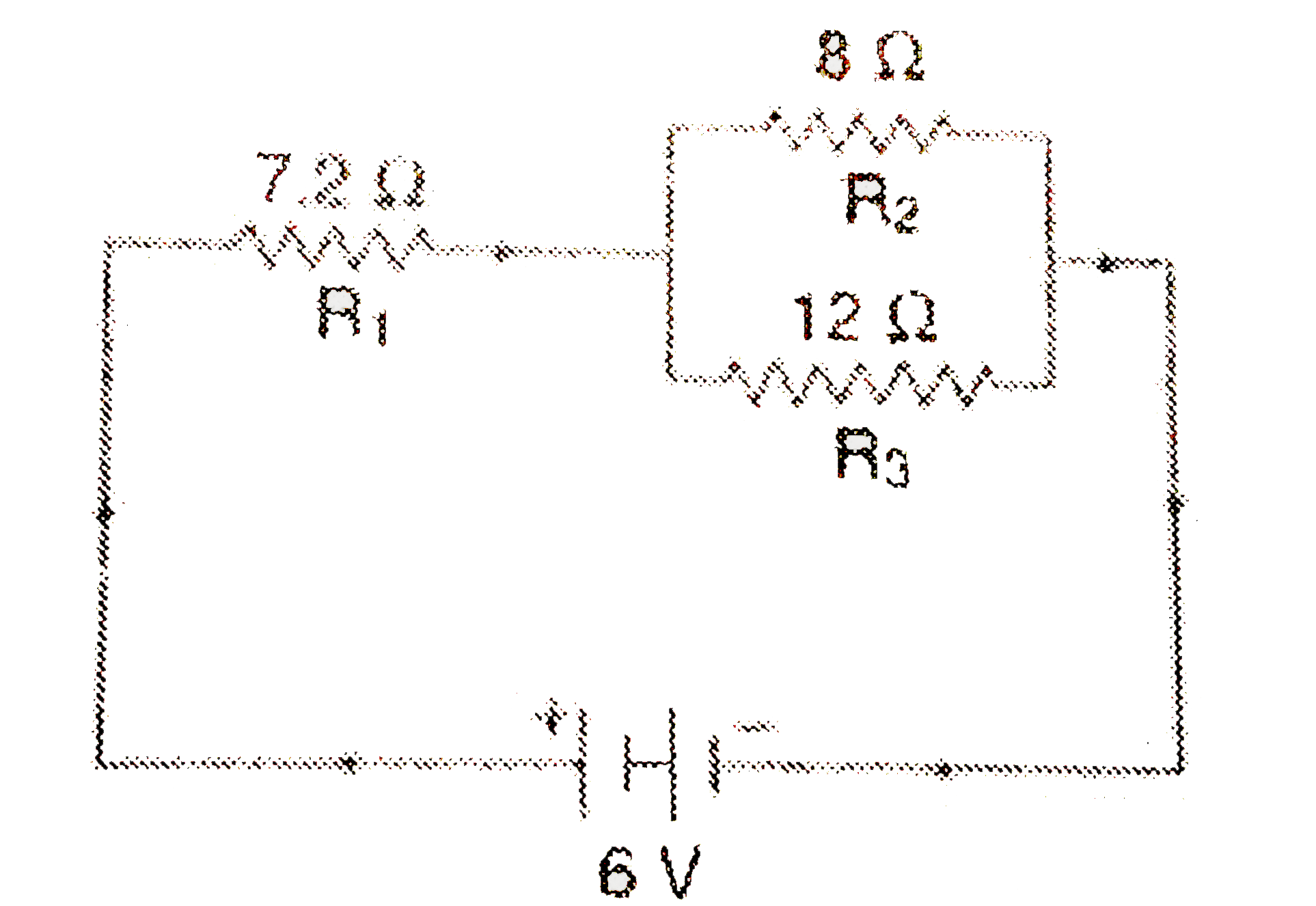
View Solution
Knowledge Check
A uniform wire of resistance R and length L is cut into four equal parts , each of lengths L/4, which are then connected in parallel combination. The effective resistance of the combination. The effective resistance of the combination will be
ARB4RCR4DR16Three resistors R1,R2 and R3 are to be combined to form an electrical circuit as shown in the figure. It is found that when R1R2andR3 are put respectively in positions A, B and C, the effective resistance of the circuit is 70 ΩWhen R2,R3andR1 are put respectively in position A, B and C the effective resistance is 35Ω and when R3,R1andR2 are respectively put in the position A, B and C, the effective resistance is 42Ω
If R1,R2andR3 are all connected in parallel, the effective resistance will beA37ΩB72ΩC50//7OmegaD607ΩThree resistors R1,R2 and R3 are to be combined to form an electrical circuit as shown in the figure. It is found that when R1R2andR3 are put respectively in positions A, B and C, the effective resistance of the circuit is 70 ΩWhen R2,R3andR1 are put respectively in position A, B and C the effective resistance is 35Ω and when R3,R1andR2 are respectively put in the position A, B and C, the effective resistance is 42Ω
IfR_(1), R_(2)and R,_(3)are put in series, the effective resistance will beA210ΩB100ΩC105ΩD11Ω
Two resistance of identical shape but of different resistivity of values 3 and 6 are connected in parallel combination .The effective resistivity of the combination is
View Solution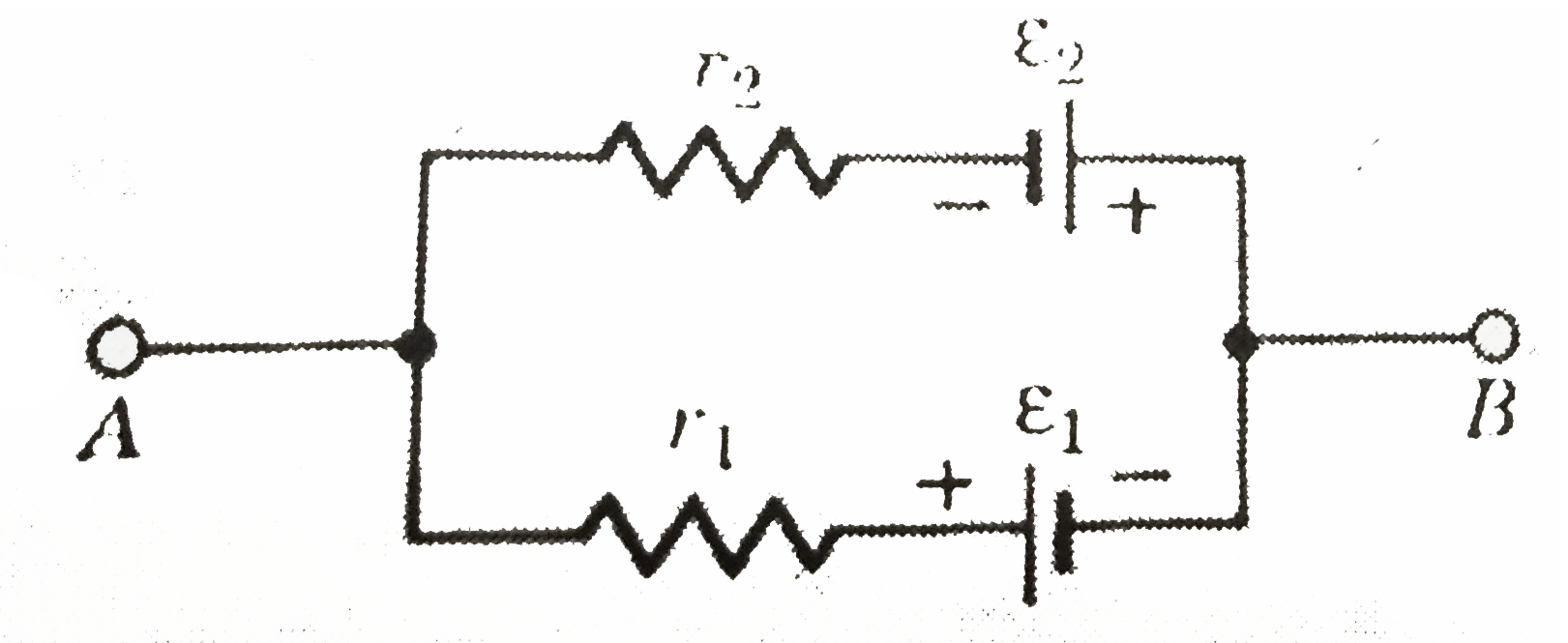
find the emf (ε0) and internal resistance (r0) if a battery which is equivalent to a parallel combination of two batteries of emfs ε1andε2 and internal resistances r1andr2 respectively, with polarities as shown in figure.
View SolutionFind the emf (V) and internal resistance (r) of a single battery which is equivalent to a parallel combination of two batteries of emf's V1,andV_(2), and internal resistance r1 and r2 respectively, with polarities as shown in the figure

View SolutionA parallel combination of two cells of emfs ε1 and ε2, and internal resistance r1 and r2 is used to supply current to a load of resistance R. Write the expression for the current through the load in terms of ε1,ε2,r1 and r2.
View SolutionFor series combination total resistance R will be:
View Solution