Shade the region represented by the inequations. x+y≤3 and 3x−2y≥4.
The correct Answer is:3x−2y≥4
To solve the problem of shading the region represented by the inequalities x+y≤3 and 3x−2y≥4, we will follow these steps:
Step 1: Rewrite the Inequalities
We have two inequalities:
1. x+y≤3
2. 3x−2y≥4
Step 2: Convert Inequalities to Equations
To find the boundary lines, we convert the inequalities into equations:
1. x+y=3
2. 3x−2y=4
Step 3: Find Intercepts for the First Equation
For x+y=3:
- When x=0, y=3 (Point: (0,3))
- When y=0, x=3 (Point: (3,0))
Step 4: Plot the First Line
Plot the points (0,3) and (3,0) on the graph and draw a solid line through these points since the inequality is less than or equal to (≤).
Step 5: Determine the Shaded Region for the First Inequality
To determine which side of the line to shade, we can test a point. Let's use the origin (0,0):
- Substitute into the inequality: 0+0≤3 (True)
Thus, we shade the region below the line x+y=3.
Step 6: Find Intercepts for the Second Equation
For 3x−2y=4:
- When x=0, −2y=4 → y=−2 (Point: (0,−2))
- When y=0, 3x=4 → x=43 (Point: (43,0))
Step 7: Plot the Second Line
Plot the points (0,−2) and (43,0) on the graph and draw a solid line through these points since the inequality is greater than or equal to (≥).
Step 8: Determine the Shaded Region for the Second Inequality
Again, we can test the origin (0,0):
- Substitute into the inequality: 3(0)−2(0)≥4 (False)
Thus, we shade the region above the line 3x−2y=4.
Step 9: Identify the Common Shaded Region
Now, we look for the common shaded region between the two inequalities. The region below the line x+y=3 and above the line 3x−2y=4 is our solution.
Final Step: Shade the Common Region
Shade the area that satisfies both inequalities on the graph.
---
We have two inequalities:
1. x+y≤3
2. 3x−2y≥4
To find the boundary lines, we convert the inequalities into equations:
1. x+y=3
2. 3x−2y=4
For x+y=3:
- When x=0, y=3 (Point: (0,3))
- When y=0, x=3 (Point: (3,0))
Plot the points (0,3) and (3,0) on the graph and draw a solid line through these points since the inequality is less than or equal to (≤).
To determine which side of the line to shade, we can test a point. Let's use the origin (0,0):
- Substitute into the inequality: 0+0≤3 (True)
Thus, we shade the region below the line x+y=3.
For 3x−2y=4:
- When x=0, −2y=4 → y=−2 (Point: (0,−2))
- When y=0, 3x=4 → x=43 (Point: (43,0))
Plot the points (0,−2) and (43,0) on the graph and draw a solid line through these points since the inequality is greater than or equal to (≥).
Again, we can test the origin (0,0):
- Substitute into the inequality: 3(0)−2(0)≥4 (False)
Thus, we shade the region above the line 3x−2y=4.
Now, we look for the common shaded region between the two inequalities. The region below the line x+y=3 and above the line 3x−2y=4 is our solution.
Shade the area that satisfies both inequalities on the graph.
Topper's Solved these Questions
- LINEAR INEQUALITIESBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - LINEAR INEQUALITIESEXERCISE - QUESTION BANK -13
20 Videos
- LINEAR INEQUALITIESBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - LINEAR INEQUALITIESEXERCISE - SELF ASSESMENT SHEET -13
10 Videos
- LINEAR EQUATIONS IN ONE VARIABLE (REVISION)BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS IN ONE VARIABLE (REVISION)EXERCISE - Self Assessment Sheet
10 Videos
- MATRICES BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - MATRICES EXERCISE - UNIT TEST -2
20 Videos
Similar Questions
Knowledge Check
The shaded region is represented by the inequation:
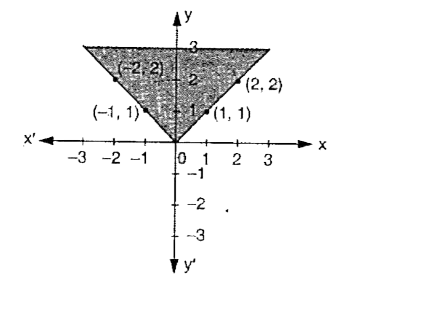 Ay≥xBy≥−xCy≥|x|Dy≤|x|
Ay≥xBy≥−xCy≥|x|Dy≤|x|The shaded region is represented by the inequality:
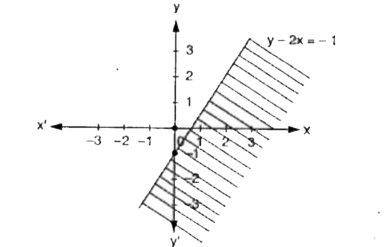 Ay−2x≤−1Bx−2y≤−1Cy−2x≥−1Dx−2y≥−1
Ay−2x≤−1Bx−2y≤−1Cy−2x≥−1Dx−2y≥−1Region represented by the inequalities x≥0,y≥0 is
Afirst quadrantBsecond quadrantCthird quadrantDfourth quadrant
Construct the region represented by the inequations x+y≤3andx−y≤2.
View SolutionConstruct the region represented by the inequation x+3y≥3and3x+y≤3
View SolutionThe region represented by the inequation system x,y≥0,y≤5,x+y≤4 is
View SolutionThe region represented by the inequations 2x+3y≤18,x+y≥10,x≥0,y≤0 is
View SolutionInequations 3x−y≥3and4x−y>4
View Solution
