The absolute value of a number is its distance from 0 on a number line. The number line representing the inequaltiy |x|<4 is


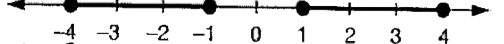
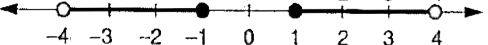
The correct Answer is:A
To solve the inequality |x| < 4, we need to understand what the absolute value means. The absolute value of a number x, denoted as |x|, represents the distance of x from 0 on the number line.
Here’s how we can solve the inequality step by step:
Step 1: Understand the definition of absolute value
The inequality |x| < 4 means that the distance of x from 0 is less than 4. This can be interpreted as x being between -4 and 4.
Step 2: Split the absolute value inequality
We can express the inequality |x| < 4 in two parts:
1. When x is positive: x < 4
2. When x is negative: -x < 4, which can be rewritten as x > -4 (after multiplying by -1 and reversing the inequality).
Step 3: Combine the inequalities
From the two parts, we have:
- From the first part: x < 4
- From the second part: x > -4
Combining these two inequalities gives us:
-4 < x < 4
Step 4: Represent the solution on a number line
On a number line, we will represent the solution -4 < x < 4. This means:
- We will place open circles (hollow circles) at -4 and 4 to indicate that these points are not included in the solution.
- The region between -4 and 4 will be shaded to show all the numbers that satisfy the inequality.
Final Answer
The number line representing the inequality |x| < 4 is shown with open circles at -4 and 4, and the region between them shaded.
---
The inequality |x| < 4 means that the distance of x from 0 is less than 4. This can be interpreted as x being between -4 and 4.
We can express the inequality |x| < 4 in two parts:
1. When x is positive: x < 4
2. When x is negative: -x < 4, which can be rewritten as x > -4 (after multiplying by -1 and reversing the inequality).
From the two parts, we have:
- From the first part: x < 4
- From the second part: x > -4
-4 < x < 4
On a number line, we will represent the solution -4 < x < 4. This means:
- We will place open circles (hollow circles) at -4 and 4 to indicate that these points are not included in the solution.
- The region between -4 and 4 will be shaded to show all the numbers that satisfy the inequality.
The number line representing the inequality |x| < 4 is shown with open circles at -4 and 4, and the region between them shaded.
Topper's Solved these Questions
- LINEAR INEQUALITIESBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - LINEAR INEQUALITIESEXERCISE - QUESTION BANK -13
20 Videos
- LINEAR EQUATIONS IN ONE VARIABLE (REVISION)BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS IN ONE VARIABLE (REVISION)EXERCISE - Self Assessment Sheet
10 Videos
- MATRICES BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - MATRICES EXERCISE - UNIT TEST -2
20 Videos
Similar Questions
Knowledge Check
Every point on a number line represents.
Aa rational numberBa natural numberCan irrational numberDa unique real number
Represent −7 on number line
View SolutionRepresent 10−3 on number line.
View SolutionRepresent 10.5 on number line
View SolutionRepresent the following numbers on the number line.
0
View SolutionRepresent 8 and −2 on a number line.
View SolutionRepresent 5 and −2 on a number line.
View SolutionRepresent 4×4 on number line.
View Solution
