Tangents PA and PB are drawn to x2+y2=9 from any arbitrary point P on the line x+y=25 . The locus of the midpoint of chord AB is (a)25(x2+y2)=9(x+y) (b)25(x2+y2)=3(x+y) (c)5(x2+y2)=3(x+y) (d) none of theseSolution in Bengali
x2+y2−2x−2y=0
x2+y2+2x+2y=0
x2+y2−2x+2y=0
x2+y2+2x−2y=0
The correct Answer is:A
Let P(a,4−a).
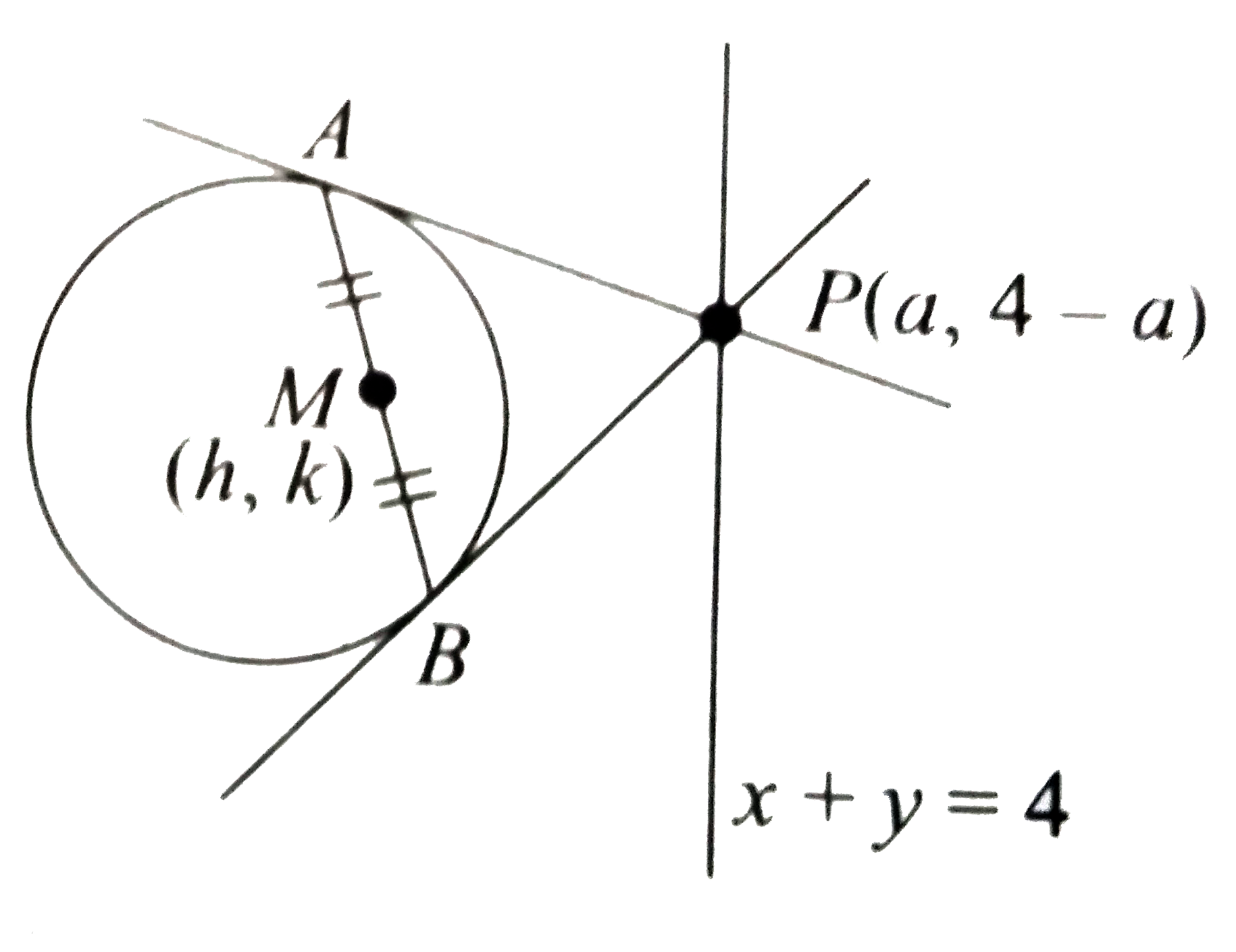
The equation of chord of contact AB is
xa+y(4−a)=8 (i)
Also, equation of chord AB whose mid-points is M(h,k) is
hx+ky=h2+k2 (ii) (using T=S1)
Since (i) and (ii) are identical, on comparing the coefficients, we get
ah=4−ak=8h2+k2=a+4−ah+k=4h+k
⇒4(h2+k2)=8(h+k)
Hence, locus of M(h,k) is x2+y2−2x−2y=0.
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type
9 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For problems 3 and 4
2 Videos
- COMPLEX NUMBERSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERSEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
Similar Questions
The line 3x+6y=k intersects the curve 2x2+3y2=1 at points AandB . The circle on AB as diameter passes through the origin. Then the value of k2 is__________
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionPARAGRAPH X Let S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let E1E2 and F1F2 be the chords of S passing through the point P0(1, 1) and parallel to the x-axis and the y-axis, respectively. Let G1G2 be the chord of S passing through P0 and having slope −1 . Let the tangents to S at E1 and E2 meet at E3 , the tangents to S at F1 and F2 meet at F3 , and the tangents to S at G1 and G2 meet at G3 . Then, the points E3, F3 and G3 lie on the curve x+y=4 (b) (x−4)2+(y−4)2=16 (c) (x−4)(y−4)=4 (d) xy=4
View SolutionLet z1 and z2 be two distinct complex numbers and z=(1−t)z1+tz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then
View SolutionTangents PA and PB are drawn to x2+y2=9 from any arbitrary point P on the line x+y=25 . The locus of the midpoint of chord AB is 25(x2+y2)=9(x+y) 25(x2+y2)=3(x+y) 5(x2+y2)=3(x+y) noneofthese
View SolutionLocus of feet of perpendicular from (5,0) to the tangents of (x^(2))/(16)-(y^(2))/(9)=1 is (A)x^(2)+y^(2)=4(B)x^(2)+y^(2)=16(C)x^(2)+y^(2)=9(D)x^(2)+y^(2)=25
View SolutionFrom a point P tangents are drawn to the elipse x2a2+y2b2=1.lf the chord of contact touches the ellipse x2c2+y2a2=1,then the locus of P is
View SolutionLet the foci of the ellipse (x^(2))/(9)+y^(2)=1 subtend a right angle at a point P. Then,the locus of P is (A) x^(2)+y^(2)=1(B)x^(2)+y^(2)=2 (C) x^(2)+y^(2)=4(D)x^(2)+y^(2)=8
View Solutionयदि A=[(x,y):x2+y2=25] तथा B=[(x,y):x2+9y2=144] , तब A∩B में है / है
View SolutionLet P be a point on the circle x2+y2=9,Q a point on the line 7x+y+3=0 , and the perpendicular bisector of PQ be the line x−y+1=0 . Then the coordinates of P are (0,−3) (b) (0,3) (7225,2135) (d) (−7225,2125)
View SolutionThe centers of a set of circles, each of radius 3, lie on the circle x2+y2=25 . The locus of any point in the set is 4≤x2+y2≤64 x2+y2≤25 x2+y2≥25 (d) 3≤x2+y2≤9
View SolutionTangents PA and PB are drawn to x2+y2=9 from any arbitrary point P on the line x+y=25 . The locus of the midpoint of chord AB is 25(x2+y2)=9(x+y) 25(x2+y2)=3(x+y) 5(x2+y2)=3(x+y) noneofthese
View SolutionFrom an arbitrary point P on the circle x2+y2=9 , tangents are drawn to the circle x2+y2=1 , which meet x2+y2=9 at A and B . The locus of the point of intersection of tangents at A and B to the circle x2+y2=9 is
(a) x2+y2=(277)2 (b) x2−y2(277)2 y2−x2=(277)2 (d) none of these
View SolutionFind the products: (3x−5y)(9x2+25y2+15xy)
View SolutionAt which point curve x^2+y^2=25 Line drawn on x^2+y^2=25 Is parallel to?
View SolutionThe locus of the midpoint of the chord of the circle x2+y2=25 which is tangent of the hyperbola x29−y216=1 is
View Solution
