Two circles are drawn through the points (a,5a)and(4a,a) to touch the y-axis. Prove that they intersect at angle tan−1(409).Solution in Bengali
tan−1(4/3)
tan−1(40/9)
tan−1(84/187)
π/4
The correct Answer is:B
Equation of any circle through the given points is:
(x−a)(x−4a)+(y−5a)(y−a)+λ(4x+3y−19a)=0, for some λ∈R.
As it touches the y-axis, putting x=0 and comparing discriminant of resulting quadratic equation in x to 0, we get
∴(−3a+3λ2)2=9a2−19λa
∴λ=0,−40a9.
∴ The required circles are
x2+y2−5ax−6ay+9a2=0
x2+y2−5ax−6ay+9a2−40a9(4x+3y−19a)=0
Hence centres are (5a2,3a) and (205a18,29a3)
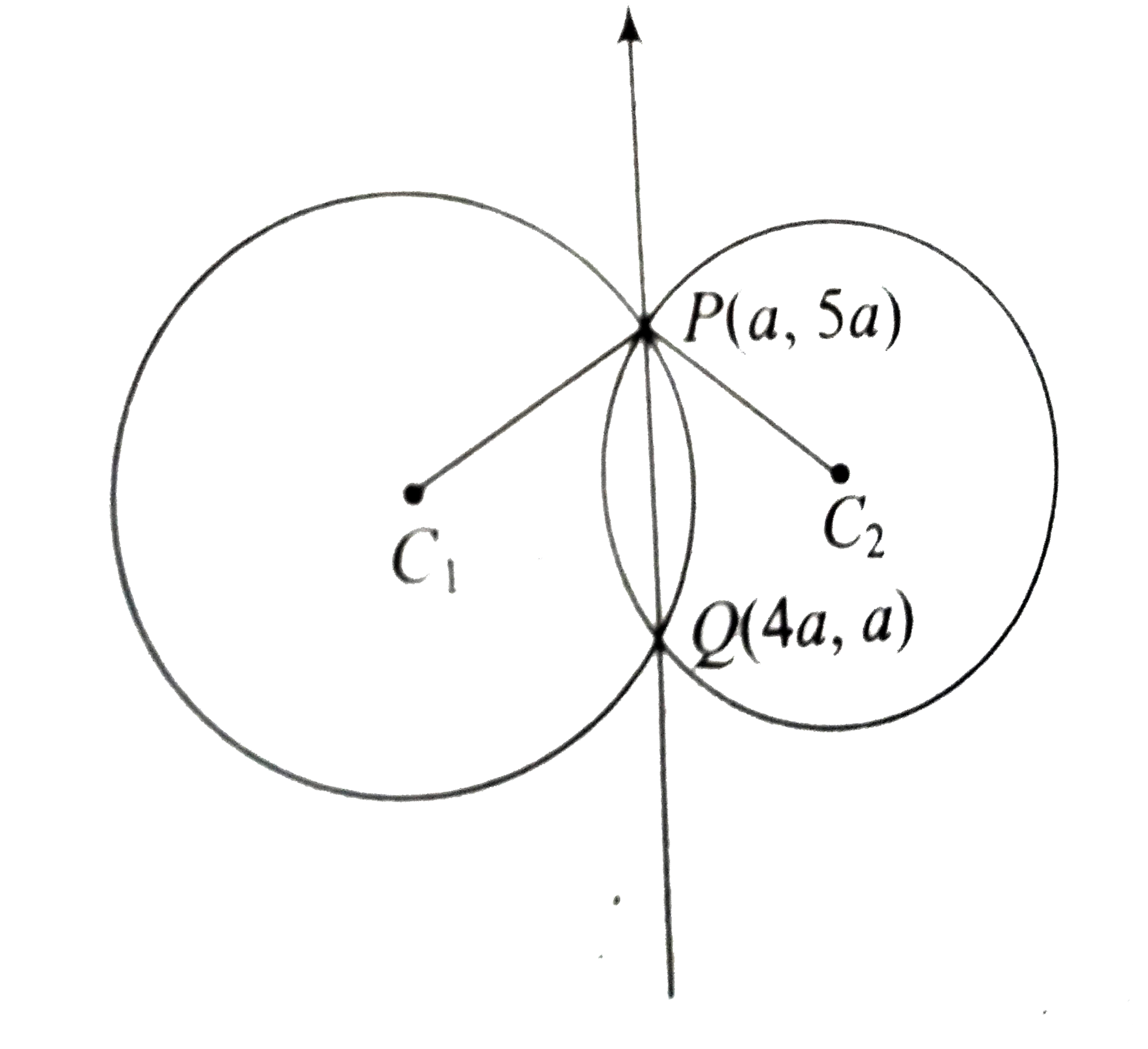
The centres of the given circles are:
C1(205a18,29a3) and C2(5a2,3a)
Now, the angle of intersection θ of these two circles is the angle between the radius vectors a the common point P to the two circles.
i.e., ∠C1PC2=θ
and slope of C2P=5a−3aa−5a2=−43
So, tanθ=84187+431−84187×43=252+748561−336=409
⇒θ=tan−1(409)
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type
9 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For problems 3 and 4
2 Videos
- COMPLEX NUMBERSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERSEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
Similar Questions
The line 3x+6y=k intersects the curve 2x2+3y2=1 at points AandB . The circle on AB as diameter passes through the origin. Then the value of k2 is__________
View SolutionPARAGRAPH X Let S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let E1E2 and F1F2 be the chords of S passing through the point P0(1, 1) and parallel to the x-axis and the y-axis, respectively. Let G1G2 be the chord of S passing through P0 and having slope −1 . Let the tangents to S at E1 and E2 meet at E3 , the tangents to S at F1 and F2 meet at F3 , and the tangents to S at G1 and G2 meet at G3 . Then, the points E3, F3 and G3 lie on the curve x+y=4 (b) (x−4)2+(y−4)2=16 (c) (x−4)(y−4)=4 (d) xy=4
View SolutionLet z1 and z2 be two distinct complex numbers and z=(1−t)z1+tz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then
View SolutionIf two intersecting chords of a circle make equal angles with the diameterpassing through their point of intersection, prove that the chords are equal
View SolutionThe circle which can be drawn to pass through (1, 0) and (3, 0) and to touch the y-axis intersect at angle θ. Then cosθ is equal to (a)12 (b) −12 (c) 14 (d) −14
View SolutionTwo circles are drawn through the points (a,5a) and (4a,a) to touch the y-axis.Prove that they intersect at angle tan ^(-1)((40)/(9))
View SolutionP(a,5a) and Q(4a,a) are two points. Two circles are drawn through these points touching the axis of y.
Centre of these circles are at
View Solutionचित्र में O एवं O' केन्द्र के दो वृत्त एक-दूसरे का बाह्यतः बिन्दु C पर स्पर्श करते है। इन वृत्तों की एक उभयनिष्ठ स्पर्श रेखा AB खींची गई है। सिद्ध कीजिए कि ∠ACB=90∘
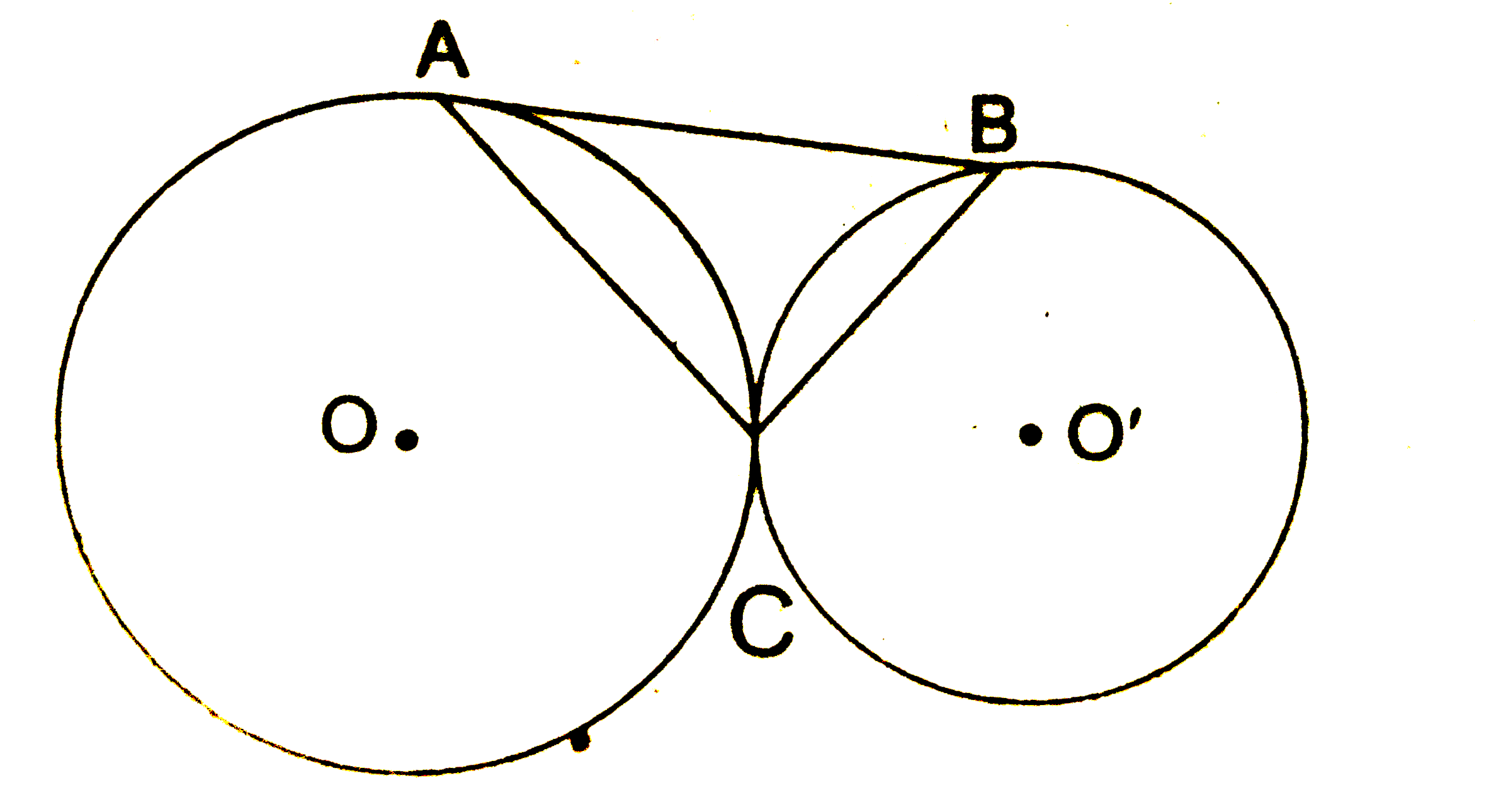
View SolutionTwo circles intersect each other at P externally. The straight QR touches the circle at two points Q and R. Prove that ∠QPR=1 right angle.
View Solutionसिद्ध कीजिए कि उस परवलय का समीकरण जिसके शीर्ष और नाभि x-अक्ष पर मूलबिंदु से क्रमशः 4a तथा 5a की दूरियों पर है,
y2=4a(x−4a) है।
View SolutionThe circles which can be drawn to pass through (3,0) and (5,0) and to touch the y-axis intersect at an angle θ , then cosθ is equal to
View Solutionகொடுக்கப்பட்ட படத்தில் O மையமாக உடைய வட்டத்தின் ஆரம் 5 செ .மீ ஆகும் .T ஆனது OT =13 செ .மீ என அமைந்த ஒரு புள்ளி மற்றும் OT ஆனது வட்டத்தை E ல் வெட்டுகிறது,வட்டத்தின் E என்ற புள்ளியின் வழியாக செல்லும் ஒரு தொடுகோடு AB எனில் ,AB -யின் நீளம் காண்க ?
View SolutionProve that the lengths of the two ji intersecting in a circle are equal if they make equal angles in the diameter passing through their point of intersection.
View SolutionIf two intersecting chords of a circle make equal angles with diameter passing through their point of intersection, prove that the chords are equal.
View SolutionIf two intersecting chords of a circle make equal angles with the diameterpassing through their point of intersection, prove that the chords are equal
View SolutionProve that if the two tangents drawn at the two points on the top of the circle intersect, then the lengths of the two straight lines drawn from the point of intersection to the point of tangent will be equal.
View Solution
