An isosceles triangle with base 24 and legs 15 each is inscribed in a circle. Find the radius Solution in Bengali
4(x2+y2)+8x−8y−73=0
2(x2+y2)+4x−4y−31=0
2(x2+y2)+4x−4y−21=0
4(x2+y2)+8x−8y−161=0
The correct Answer is:D
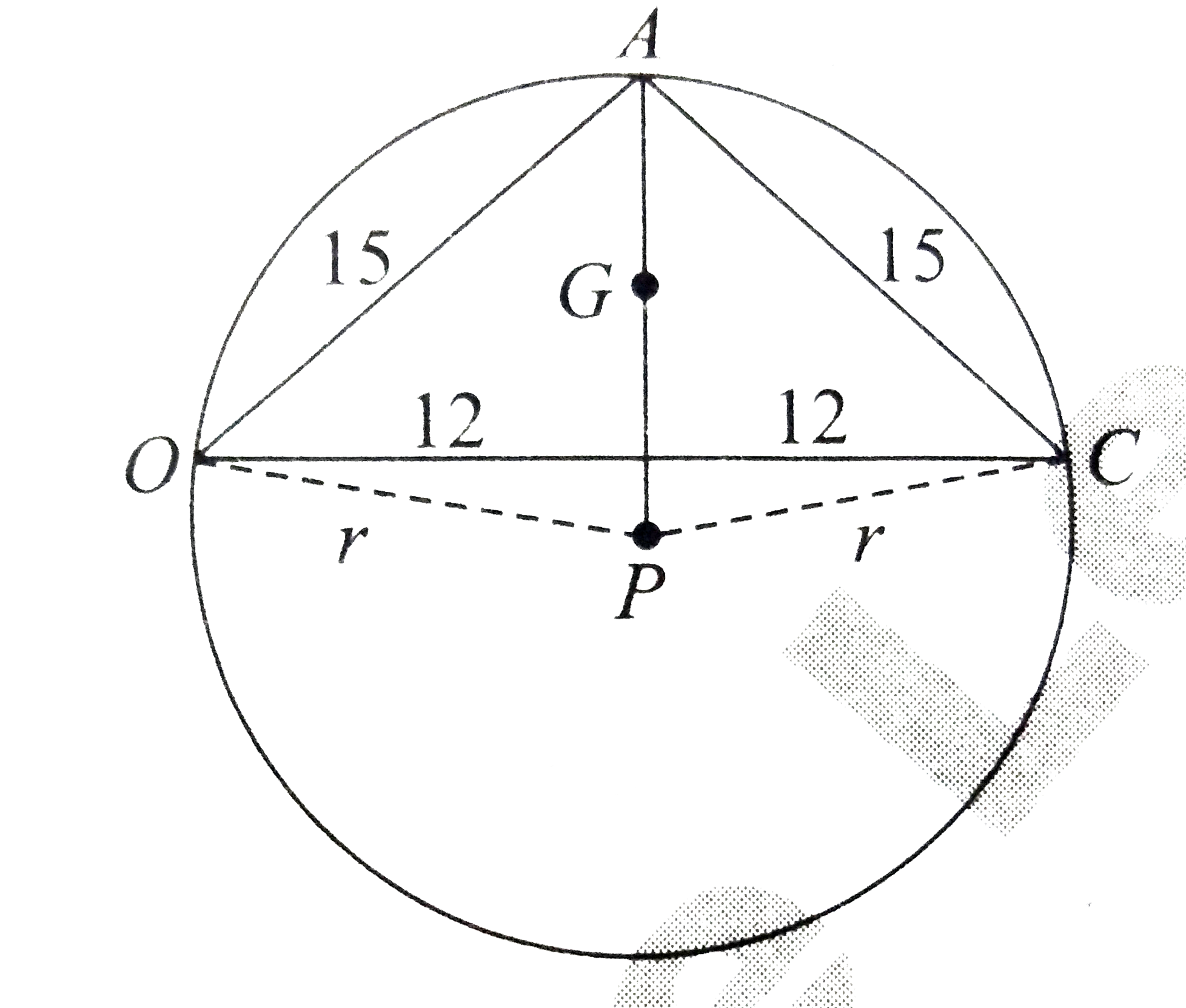
(r−9)2+122=r2
⇒81−18r+144=0
⇒r=25518=252
Locus is a concentric circle with radius PG.
PG=(r−9)+13(9)
=r−6
=252−6=132
Lcus is (x+1)2+(y−1)2=(132)2
⇒x2+y2+2x−2y−1614=0
Topper's Solved these Questions
- CIRCLESBook:CENGAGE PUBLICATIONChapter:CIRCLESExercise:Multiple Correct Answers Type
Explore 9 Videos
- CIRCLESBook:CENGAGE PUBLICATIONChapter:CIRCLESExercise:Comprehension Type
Explore 8 Videos
- CIRCLE Book:CENGAGE PUBLICATIONChapter:CIRCLE Exercise:For problems 3 and 4
Explore 2 Videos
- COMPLEX NUMBERSBook:CENGAGE PUBLICATIONChapter:COMPLEX NUMBERSExercise:MULTIPLE CORRECT ANSWER TYPE
Explore 6 Videos
Similar Questions
The line 3x+6y=k intersects the curve 2x2+3y2=1 at points AandB . The circle on AB as diameter passes through the origin. Then the value of k2 is__________
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionPARAGRAPH X Let S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let E1E2 and F1F2 be the chords of S passing through the point P0(1, 1) and parallel to the x-axis and the y-axis, respectively. Let G1G2 be the chord of S passing through P0 and having slope −1 . Let the tangents to S at E1 and E2 meet at E3 , the tangents to S at F1 and F2 meet at F3 , and the tangents to S at G1 and G2 meet at G3 . Then, the points E3, F3 and G3 lie on the curve x+y=4 (b) (x−4)2+(y−4)2=16 (c) (x−4)(y−4)=4 (d) xy=4
View SolutionLet z1 and z2 be two distinct complex numbers and z=(1−t)z1+tz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then
View SolutionIf an isosceles triangle ABC in which AB=AC=6cm is inscribed in a circle of radius 9cm, find the area of the triangle.
View SolutionA right angled isosceles triangle is inscribed in a semi-circle of radius 7cm. The area enclosed by the semi-circle but exterior to the triangle is:
View SolutionAn isosceles triangle with base 24 and legs 15 each is inscribed in a circle with centre at (-1,1). The locus of the centroid of that Delta is
View SolutionABC किसी वृत्त में अंकित समद्विबाहु त्रिकोण है यदि AB=AC=12√5 तथा BC=24 सेमी है तो वृत्त की त्रिज्या क्या होगी ?
View SolutionInscribed in a circles is an isosceles triangle ABC whose base AC=b and the base angle is α. A second circle touches the first circle and the base of the triangle at its midpoint D, and is situated outside the triangle. Find the radius of the second circle.
View SolutionA circle of radius unity is inscribed in an isosceles triangle. The least perimeter of the triangle is :
View Solutionদেখাও যে, একটি প্রদত্ত বৃত্তে অন্তর্লিখিত সমদ্বিবাহু ত্রিভুজসমূহের মধ্যে সমবাহু ত্রিভুজের পরিসীমা বৃহত্তম।
View SolutionThe radius of the circumcircle of a right angled triangle is 15 cm and the radius of its inscribed circle is 6 cm. Find the sides of the triangle.
View SolutionIf an isosceles triangle ABC , in which AB = AC = 10 cm , is inscribed in a circle of radius 10 cm , find the area of the triangle .
View SolutionIf an isosceles ΔABC in which AB=AC=6cm is inscribed in a circle of radius 9 cm, find the area of the triangle.
View SolutionAn isosceles triangle with base 24 and legs 15 each is inscribed in a circle with centre at (−1,1). The locus of the centroid of that Δ is
View SolutionThe least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is
View Solution
