If the radius of the circle touching the pair of lines 7x2−18xy+7y2=0 and the circle x2+y2−8x−8y=0, and contained in the given circle is equal to k, then k2 is equal toSolution in Bengali
10
9
8
7
The correct Answer is:C
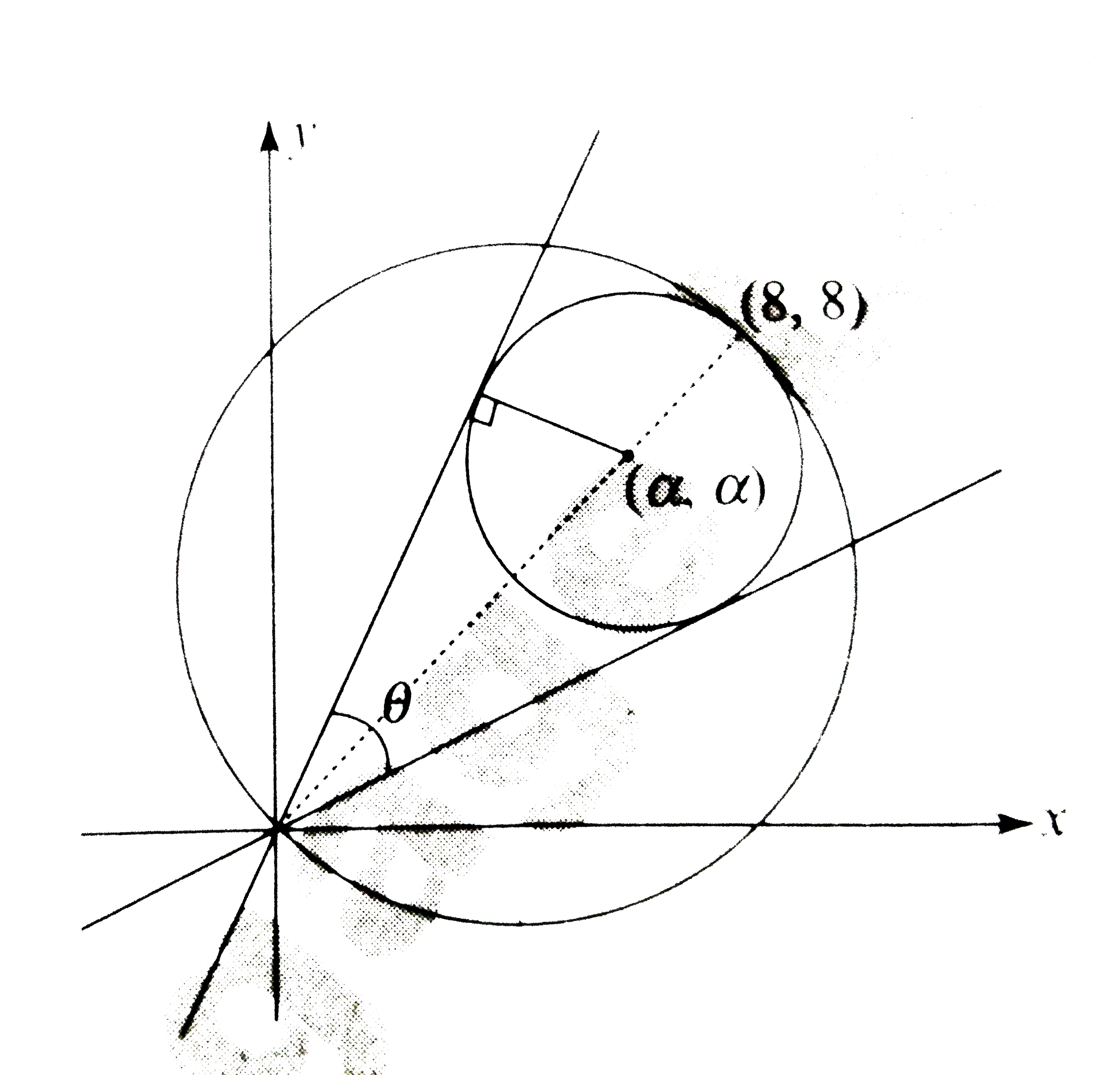
tanθ=∣∣∣2√h2−aba+b∣∣∣=4√27
∴tan.θ2=12√2
∴sin.θ2=13=√2(8−α)√2α
∴α=6
Hence, equation of circle is (x−6)2+(y−6)2=8.
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type
9 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For problems 3 and 4
2 Videos
- COMPLEX NUMBERSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERSEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
Similar Questions
The line 3x+6y=k intersects the curve 2x2+3y2=1 at points AandB . The circle on AB as diameter passes through the origin. Then the value of k2 is__________
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionPARAGRAPH X Let S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let E1E2 and F1F2 be the chords of S passing through the point P0(1, 1) and parallel to the x-axis and the y-axis, respectively. Let G1G2 be the chord of S passing through P0 and having slope −1 . Let the tangents to S at E1 and E2 meet at E3 , the tangents to S at F1 and F2 meet at F3 , and the tangents to S at G1 and G2 meet at G3 . Then, the points E3, F3 and G3 lie on the curve x+y=4 (b) (x−4)2+(y−4)2=16 (c) (x−4)(y−4)=4 (d) xy=4
View SolutionLet z1 and z2 be two distinct complex numbers and z=(1−t)z1+tz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then
View Solutionif the line 3x-4y-k=0 touches the circle x^(2)+y^(2)-4x-8y-5=0 at (a,b), find (k+a+b)/5is
View SolutionIf the circle x^(2)+y^(2)+8x-4y+c=0 touches the circle x^(2)+y^(2)+2x+4y-11=0 externally and cuts the circle x^(2)+y^(2)-6x+8y+k=0 orthogonally then k
View SolutionIf the line hx+ky=(1)/(a) touches the circle x^(2)+y^(2)=a^(2) then the locus of (h,k) is circle of radius
View SolutionIf the line 3x−4y−k=0(k>0) touches the circle x2+y2−4x−8y−5=0 at (a, b) then k+a+b is equal to :-
View SolutionThe point (-1,0) lies on the circle x2+y2−4x+8y+k=0. The radius of the circle is
View SolutionIf the circle x2+y2+8x−4y+c=0 touches the circle x2+y2+2x+4y−11=0 externally and cuts the circle x2+y2−6x+8y+k=0 orthogonally then k =
View SolutionThe equation of the radical axis of the pair of circles 7x2+7y2−7x+14y+18=0 and 4x2+4y2−7x+8y+20=0 is :
View Solutionउन वृत्तों के केन्द्र, जो वृत्त x2+y2−8x−8y−4=0 को बाह्य रूप से स्पर्श करते हैं तथा.X-अक्ष को भी स्पर्श करते हैं, स्थित हैं
View Solutionx2+y2–8x−8y−4=0বৃত্তকে বহিঃস্পর্শ এবং x-অক্ষকে স্পর্শ করে এমন বৃত্তের কেন্দ্রগুলি অবস্থিত হবে—
View SolutionIf the circle x2+y2+8x−4y+c=0 touches the circle x2+y2+2x+4y−11=0 externally and cuts the circle x2+y2−6x+8y+k=0 orthogonally then k =
View SolutionIf the circle x2+y2−6x−8y+(25−a2)=0 touches the axis of ,y then a equals.
View SolutionIf the circle x2+y2−6x−8y+(25−a2)=0 touches the axis of x, then a equals
View Solution
