From a point P outside a circle with centre at C, tangents PA and PB are drawn such that 1(CA)2+1(PA)2=116, then the length of chord AB is Solution in Bengali
6
8
4
12
The correct Answer is:B
tanθ=rPA
Given, 1r2+1PA2=116
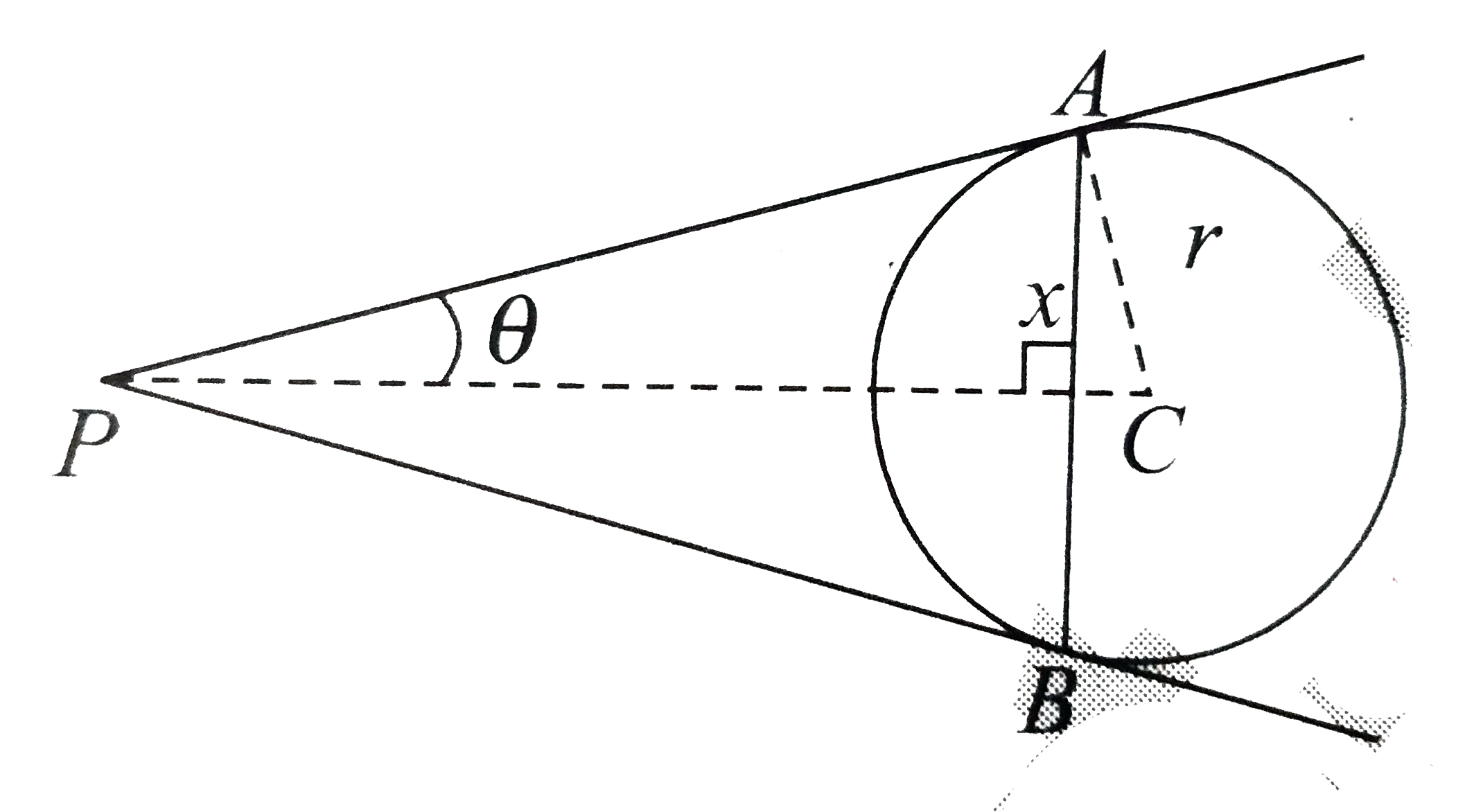
⇒cot2θ+1(PA)2=116
⇒PAsinθ=4=x⇒2x=8.
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type
9 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For problems 3 and 4
2 Videos
- COMPLEX NUMBERSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERSEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
Similar Questions
The line 3x+6y=k intersects the curve 2x2+3y2=1 at points AandB . The circle on AB as diameter passes through the origin. Then the value of k2 is__________
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionPARAGRAPH X Let S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let E1E2 and F1F2 be the chords of S passing through the point P0(1, 1) and parallel to the x-axis and the y-axis, respectively. Let G1G2 be the chord of S passing through P0 and having slope −1 . Let the tangents to S at E1 and E2 meet at E3 , the tangents to S at F1 and F2 meet at F3 , and the tangents to S at G1 and G2 meet at G3 . Then, the points E3, F3 and G3 lie on the curve x+y=4 (b) (x−4)2+(y−4)2=16 (c) (x−4)(y−4)=4 (d) xy=4
View SolutionLet z1 and z2 be two distinct complex numbers and z=(1−t)z1+tz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then
View SolutionTangents PA and PB are drawn to a circle with point P outside the circle,line joining P and centre intersect chord AB at M then,Prove that /_OPA=/_OAM
View SolutionFrom a point P outside a circle with centre at C,tangents PA and PB are drawn such that (1)/((CA)^(2))+(1)/((PA)^(2))=(1)/(16), then the length of chord AB is
View SolutionPA and PB are two tangents drawn from an external point P to a circle with centre C and radius=4cm If PA⊥PB then length of each tangent is
View SolutionIf PA and PB are tangents from an outside point P such that PA=10cm and ∠APB=60o . Find the length of chord AB .
View SolutionFrom a point P outside a circle with centre at C, tangents PA and PB are drawn such that 1(CA)2+1(PA)2=116, then fid the length of chord AB.
View SolutionFrom a point P, two tangents PA and PB are drawn such that PA=9 cm and ∠APB=60∘. Find the length of chord AB.
View SolutionFrom a point P outside a circle with centre O, tangents PA and PB are drawn to the circle. Prove that OP is the right bisector of the line segment AB.
View Solutionकिसी वृत्त के बाह्य बिंदु P से स्पर्श रेखाएं PA एवं PB खींची गयी है। यदि PA = 8 cm तो PB की लम्बाई होगी -
View Solutionकिसी वृत्त के बाह्म बिंदु P से वृत्त पर दो स्पर्श रेखाएँ PA तथा PB खींची गई हैं। यदि PA=6 सेमी हो तो PB की लम्बाई क्या होगी?
View Solutionदी आकृति में, PA और PB एक वृत्त की बाह्य बिन्दु P से स्पर्श रेखायें है। यदि PA = 4 सेमी और ∠BAC=135∘, तो जीवा AB की लम्बाई ज्ञात कीजिए।

View Solutionबिन्दु P से दो स्पर्श रेखायें PA और PB इस प्रकार खींची गई है कि PA =9 सेमी ∠APB=60∘ है। जीवा AB की लम्बाई ज्ञात कीजिए।
View SolutionA variable point P is chosen on the straight line x + y = 4 and tangents PA and PB are drawn from it to circle x2+y2=1 . Then the position of P for the smallest length of chord of contact AB is
View Solution
