Orthocenter and circumcenter of a ΔABC are (a,b)and(c,d) , respectively. If the coordinates of the vertex A are (x1,y1), then find the coordinates of the middle point of BC.Solution in Bengali
Given are the orthocentre H(a,b) and the circumcentre O(c,d).
∴ Centroid, G=(2c+a2+1,2d+b2+1)≡(2c+a3,2d+b3)
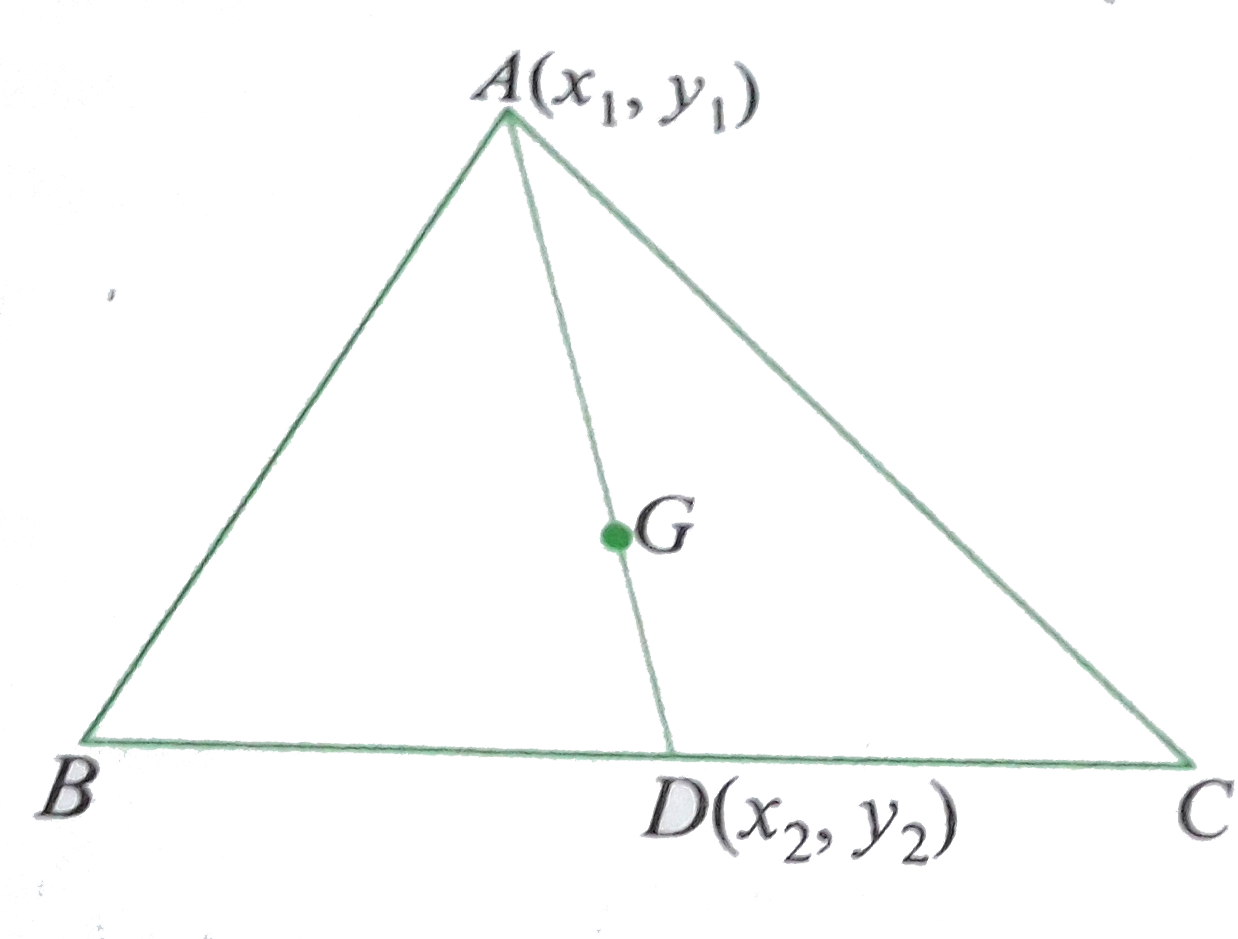
Now, centroid G divides AD in the ratio 2:, where D is the midpoint of BC.
∴2c+a3=2x2+x13
and 2d+b3=2y2+y−13
∴x2=2c+a−x12,y2=2d+b−y12
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.361videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.371videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.341videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
If a vertex of a triangle is (1,1) , and the middle points of two sides passing through it are −2,3) and (5,2), then find the centroid of the triangle.
06:31View SolutionThe vertices of a triangle are A(−1,−7),B(5,1)andC(1,4). If the internal angle bisector of ∠B meets the side AC in D, then find the length AD.
01:32View SolutionIf the circumcenter of an acute-angled triangle lies at the origin and the centroid is the middle point of the line joining the points (a2+1,a2+1) and (2a,−2a), then find the orthocentre.
05:07View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
03:25View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
08:37View SolutionA triangle has its three sides equal to a,bandc . If the coordinates of its vertices are A(x1,y1),B(x2,y2)andC(x3,y3), show that ∣∣ ∣ ∣∣x1y12x2y22x3y32∣∣ ∣ ∣∣2=(a+b+c)(b+c−a)(c+a−b)(a+b−c)
01:06View SolutionOrthocenter and circumcenter of a DeltaABC are (a,b)and(c,d) , respectively. If the coordinates of the vertex A are (x1,y1), then find the coordinates of the middle point of BC.
06:58View SolutionIn Fig.,delta ABC is an equilateral triangle with coordinates of B and C as B(1,0) and C(5,0) . Find the coordinates of vertex A
05:30View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of ABC. Then DEF is congruent to triangle. ABC (b) AEF (c) BFD, CDE (d) AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
06:27View SolutionIn fig. 28.7 if the coordinates of point P are (a,b,c) then Write the coordinates of points A, B, C, D, E and F. Write the coordinates of the feet of the perpendiculars from the point P to the coordinate axes. Write the coordinates of the feet of the perpendicular from the point P on the coordinate planes XY, YZ and ZX. Find the perpendicular distances of point P from XY,YZ and ZX− planes. Find the perpendicular distances of the point P fro the coordinate axes. Find the coordinates of the reflection of P are (a,b,c) . Therefore OA=a, OB=b nd OC=⋅
05:07View SolutionFind the coordinates of points A, B, C, D in Figure.
03:34View SolutionA, B, C, D একটি সামান্তরিকের চারটি শীর্ষবিন্দু। যদি A, B এবং C এর স্থানাঙ্ক যথাক্রমে (0,0,0), (3,-4,4) এবং (7,1,4) হয় তবে দিক অনুপাত এর সাহায্যে D শীর্ষবিন্দুর স্থানাঙ্ক নির্ণয় করো।
04:40View SolutionA(x1,y1),B(x2,y2) ಮತ್ತು C(x3,y3) ಗಳು △ABC ಯ ಶೃಂಗ ಬಿಂದುಗಳಾದರೆ ತ್ರಿಭುಜದ ಗುರುತ್ವಕೇಂದ್ರದ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ .
03:01View SolutionD,E,andF are the middle points of the sides of the triangle ABC , then (a) centroid of the triangle DEF is the same as that of ABC (b) orthocenter of the tirangleDEF is the circumcentre of ABC
04:27View SolutionOrthocenter and circumcenter of a ΔABC are (a,b)and(c,d) , respectively. If the coordinates of the vertex A are (x1,y1), then find the coordinates of the middle point of BC.
01:06View SolutionOrthocenter and circumcenter of a triangleABC are (a,b)and(c,d) , respectively. If the coordinates of the vertex A are (x1,y1), then find the coordinates of the middle point of BC.
04:29View Solution