If a vertex of a triangle is (1,1) , and the middle points of two sides passing through it are −2,3) and (5,2), then find the centroid of the triangle.Solution in Bengali
Let E and F be the midpoints of AB and AC. Let the coordinates of B and C be (α,β) and (γ,δ) respectively. Then −2=1+α2,3=1+β2,
5=1+γ2,2=1+δ2
∴α=−5,β=5,γ=9,δ=3
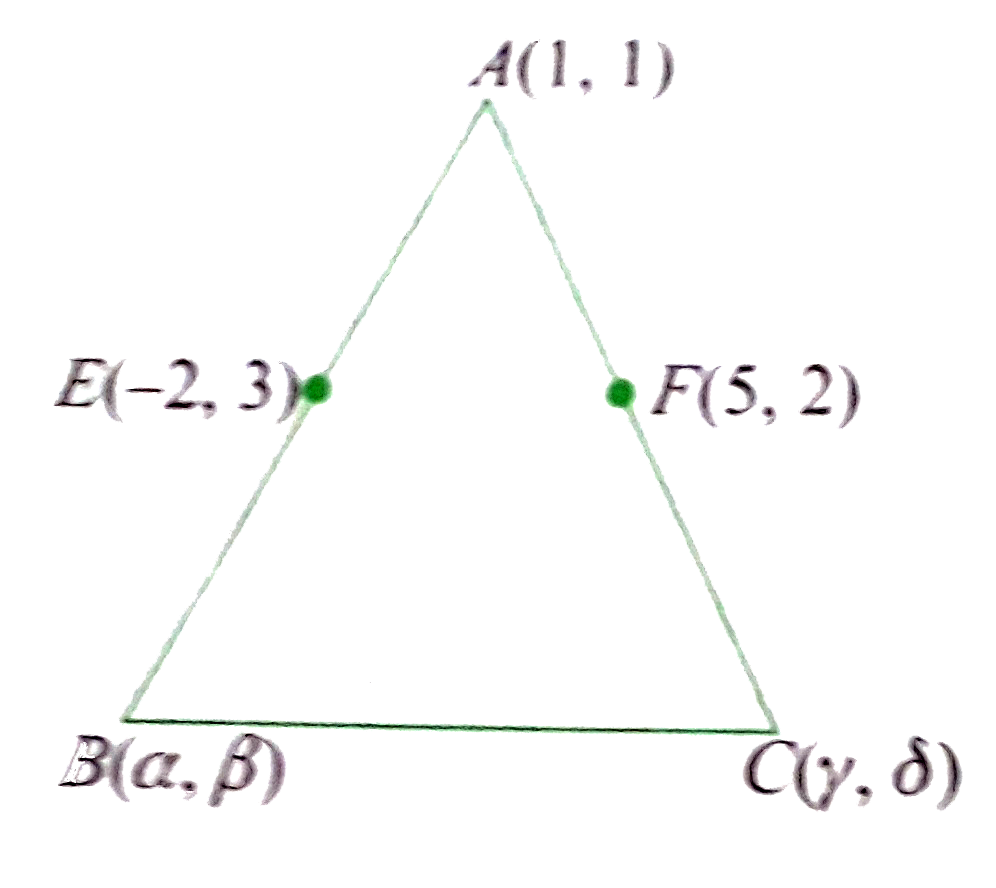
Therefore, the coordinates of B and C are (−5,5) and (9,3), respectively.
Then the centroid is
(1−5+93,1+5+93)≡(53,3)
and a=BC=√(−5−9)2+(5−3)2=10√2
b=CA=√(9−1)2+(3−1)2=2√17
c=AB=√(1+5)2+(1−5)2=2√13
Then, the incenter is
(10√2(1)+2√17(−5)+2√13(9)10√2+2√17+2√13,10√2(1)+2√17(5)+2√13(3)10√2+2√17+2√13)
i.e., (5√2−5√17+9√135√2+√17+√13,5√2+5√17+3√135√2+√17+√13)
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.37
1 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.38
1 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.35
1 Videos
- COORDINATE SYSTEMBOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
The vertices of a triangle are A(−1,−7),B(5,1)andC(1,4). If the internal angle bisector of ∠B meets the side AC in D, then find the length AD.
View SolutionDetermine x so that the line passing through (3,4)and(x,5) makes an angle of 1350 with the positive direction of the x-axis.
View SolutionOrthocenter and circumcenter of a ΔABC are (a,b)and(c,d) , respectively. If the coordinates of the vertex A are (x1,y1), then find the coordinates of the middle point of BC.
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionIf a vertex of a triangle is (1,1) , and the middle points of two sides passing through it are −2,3) and (5,2), then find the centroid and the incenter of the triangle.
View SolutionIf the middle points of the sides of a triangle are (−2,3),(4,−3),and(4,5) , then find the centroid of the triangle.
View Solution21. If a vertex of a triangle is (1, 1) and the midpoints of two sides of the triangle through this vertex are (-1, 2) and (3, 2), then the centroid of the triangle is
View SolutionIf a vertex of a triangle be (1, 1) and the middle points of the sides through it be (−2, 3) and (5, 2) , find the other vertices.
View SolutionA triangle having a vertex as (1,2) has mid-point of sides passig from this vertex as (−1,1) and (2,3) thent he centroid of the triangle is
View SolutionIf the vertex of a triangle is (1,1) and the mid-points of two sides therough this vertex are (−1,2)and(3,2) then the centroid of the triangle is-
View SolutionIf the vertex of a triangle is (1,1) and the the mid - points of two sides through this vetex are (-1,2) and (3,2) , them find the coordinates of the centroid of the triangle .
View Solutionयदि किसी त्रिभुज का एक शीर्ष {1,1} है, और इस शीर्ष से होकर जाने वाली दोनों भुजाओं के मध्यबिंदु {-1,2} व {3,2} है, तो त्रिभुज का केन्द्रक होगा|
View SolutionIf a vertex of a triangle is (1,1) , and the middle points of two sides passing through it are −2,3) and (5,2), then find the centroid of the triangle.
View SolutionIf a vertex of a triangle is (1,1) , and the middle points of two sides passing through it are −2,3) and (5,2), then find the centroid and the incenter of the triangle.
View SolutionA vertex of a triangle (1,2) Is at the midpoint of the two arms that pass through it (-1,1) And (2,3) Is the center of this triangle
View Solution
