The vertex A of ΔABC is (3,-1). The equation of median BE and angle bisector CF are x-4y+10=0 and 6x+10y-59=0, respectively. Equation of AC isSolution in Bengali
5x+18y=37
15x+8y=37
15x-8y=37
15x+8y+37=0
The correct Answer is:B
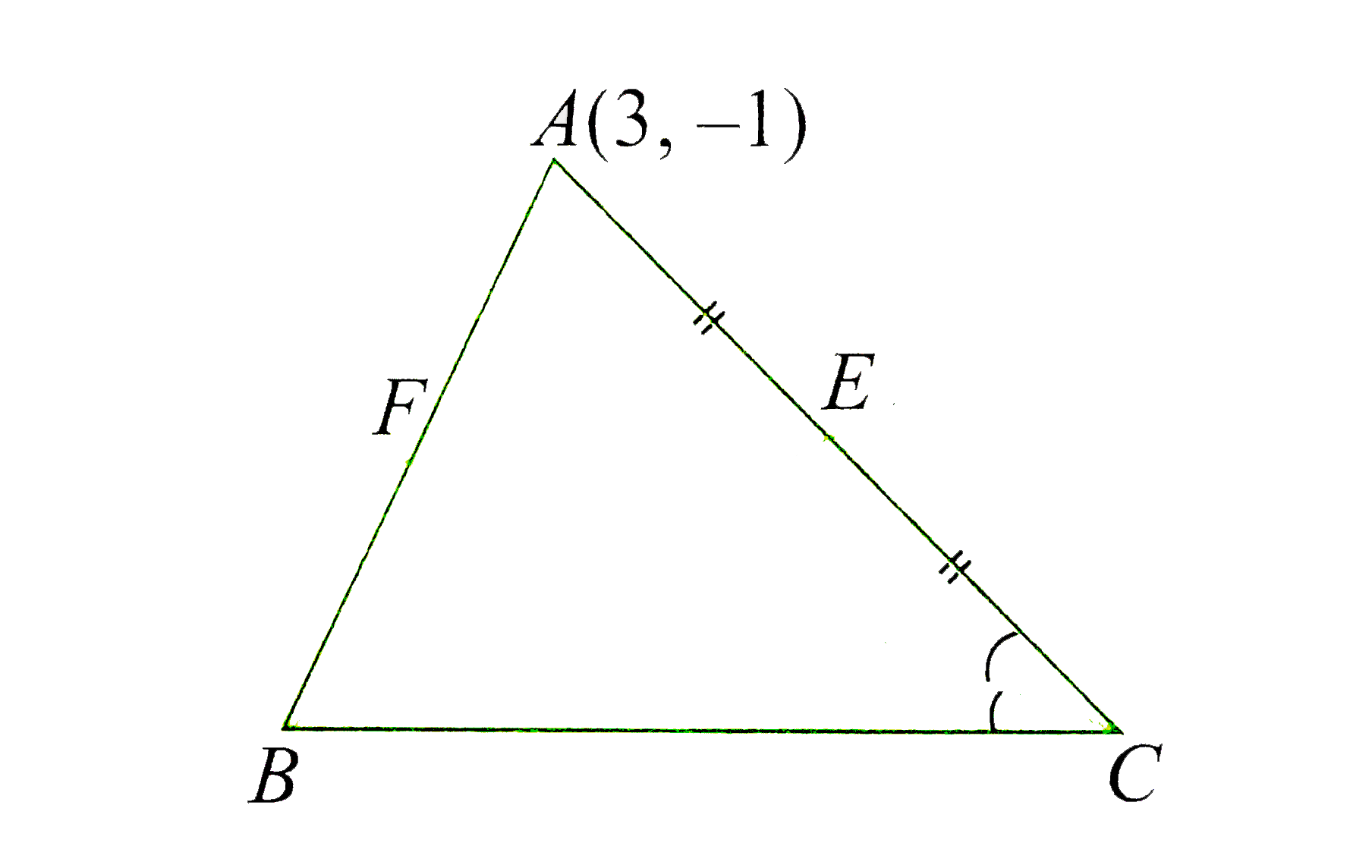
Point E is on the median x-4y+10=0.
∴E≡(x1,x1+104)
Point C is on the bisector 6x+10y-59=0.
∴C≡(x2,59−6x210)
Midpoint of AC is E.
∴x2+32=x1
⇒x2=2x1−3 (1)
and 59−6x210−12=x1+104
⇒49−6(2x1−3)20=x1+104
⇒49−12x1+18=5x1+50
⇒17x1=17
∴x1=1
Coordinates of E are (1,114).
Equation of AC is
(y+1)=114+1−2=(x−3)
⇒−8y−8=15x−45
⇒15x+8y=37
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
30 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)
27 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
View SolutionLet l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionIn /_ABC, vertex A is (1,2). If the internal angle bisector of /_B is 2x-y+10=0 and the perpendicular bisector of AC is y=x ,then find the equation of BC
View SolutionLet ABC be a triangle such that the coordinates of the vertex A are (3,1). Equation of the median through B is 2x+y-3=0 and equation of the angular bisector of C is 7x-4y-1=0. Find the slope of line BC.
View SolutionFind the equations of the sides of the triangle having (3,-1) as a vertex,x-4y+10=0 and 6x+10y-59=0 being the equations of ram angle bisetor and a median respectively drawn from different vertices.
View SolutionThe vertex A of ΔABC is (3,-1). The equation of median BE and angle bisector CF are x-4y+10=0 and 6x+10y-59=0, respectively. Equation of AC is
View SolutionLet the equations of perpendicular bisectors of sides ACandofΔABCbex+y=3andx−y=1 respectively Then vertex A is is (0,0)
The orthocentre of ΔABC is
View SolutionLet the equations of perpendicular bisectors of sides ACandofΔABCbex+y=3andx−y=1 respectively Then vertex A is is (0,0)
The circumcentre of the ΔABC is
View SolutionThe equation of perpendicular bisectors of AB and AC of a triangle ABC are x-y-5=0 and x+2y=0 respectively. If A=(1,-2) then the equation of ¯¯¯¯¯¯BC is
View SolutionIn △ABC, vertex A is (1, 2). If the internal angle bisector of ∠B is 2x−y+10=0 and the perpendicular bisector of AC is y = x, then find the equation of BC
View SolutionIn △ABC, vertex A is (1, 2). If the internal angle bisector of ∠B is 2x−y+10=0 and the perpendicular bisector of AC is y = x, then find the equation of BC
View SolutionThe vertex A of ΔABC is (3,-1). The equation of median BE and angle bisector CF are x-4y+10=0 and 6x+10y-59=0, respectively. Equation of AC is
View Solutionत्रिभुज ABC की भुजाओं AB एवं AC के लम्बो के समीकरण क्रमशः x−y−4=0 एवं 2x−y−5=0 है यदि शीर्ष A के निर्देशांक (−2,3) है तथा लम्ब समद्विभाजकों का प्रतिच्छेद बिन्दु (32,52) हो, तो क्रमशः AB एवं AC की माध्यिकाओं के समीकरण ज्ञात कीजिये।
View Solution
