Given A=(1,1) and AB is any line through it cutting the x-axis at B. If AC is perpendicular to AB and meets the y-axis in C , then the equation of the locus of midpoint P of BC is (a) x+y=1 (b) x+y=2 (c) x+y=2xy (d) 2x+2y=1Solution in Bengali
x+y=1
x+y=2
x+y=2xy
2x+2y=1
The correct Answer is:A
The equation of line AB is y-1 = m(x-1). Therefore, the equation of line AC is
y−1=−1m(x−1)
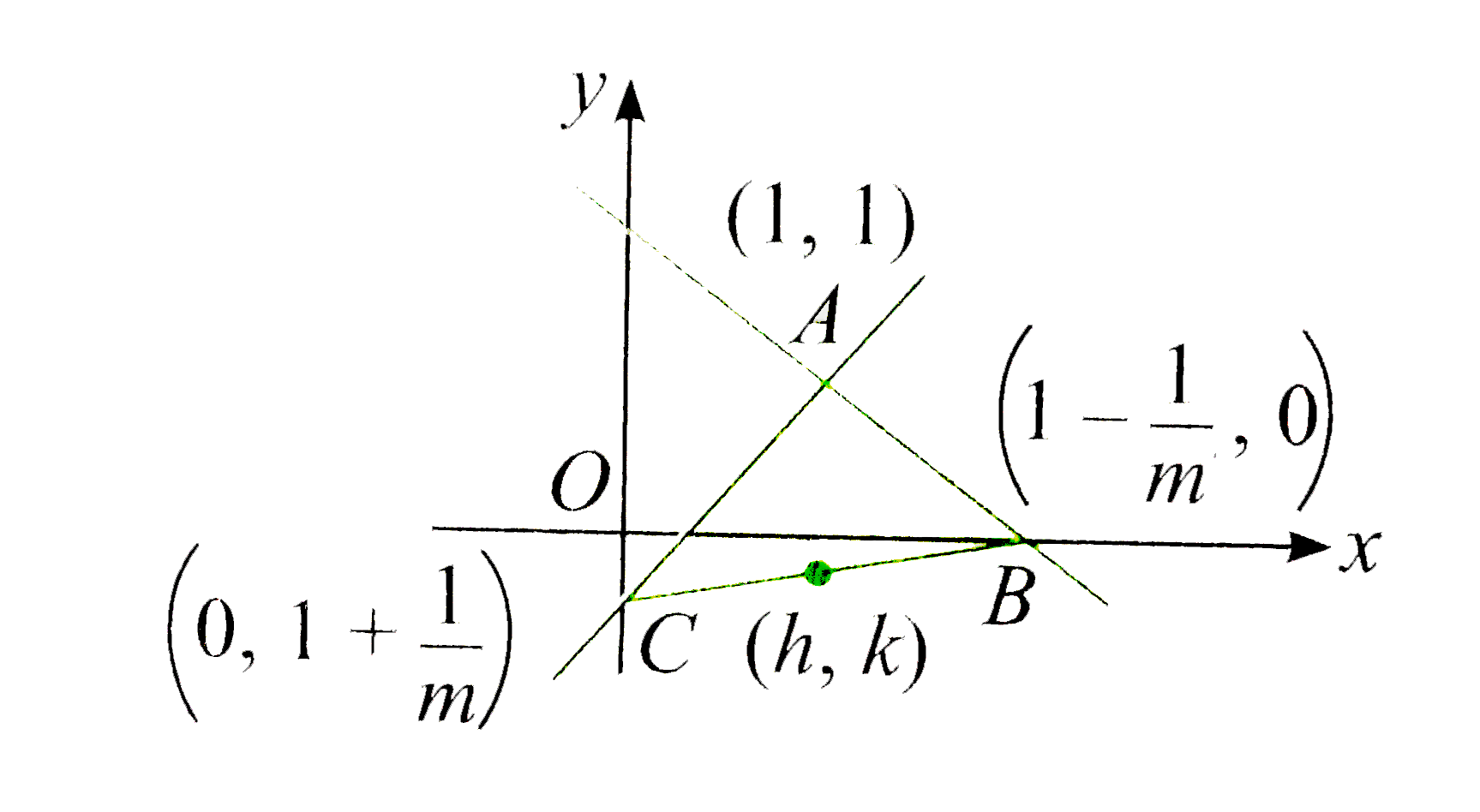
2h=1−1m
2k=1+1m
Eliminating m, we have locus x+y=1.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)30videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)27videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.65videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
04:31View SolutionLet l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
07:05View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
05:41View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
06:02View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
07:07View SolutionGiven A≡(1,1) and AB is any line through it cutting the x-axis at B. If AC is perpendicular to AB and meets the y-axis in C , then the equation of the locus of midpoint P of BC is (a) x+y=1 (b) x+y=2 (c) x+y=2xy (d) 2x+2y=1
05:52View SolutionThe equation of the line that passes through (10,−1) and is perpendicular to y=x24−2 is (a)4x+y=39 (b) 2x+y=19 (c)x+y=9 (d) x+2y=8
05:59View SolutionIf the common tangents of hyperbola x^2/4-y^2/1=lambda and the parabola y^2=4x cuts the coordinate axis at A and B, then locus of midpoint of AB is (A) y^2 = -2x (B) 2y^2 =-x (C) x^2 - y^2 =2 (D) y^2 =x
05:21View SolutionThe locus of the centre of the circle passing through (1,1) and cutting x2+y2=4 orthogonally is : (A) x+y=3 (B) x+2y=3 (C) 2x+y=3 (D) 2x−y=3
02:03View SolutionConsider the parabola P touching x-axis at (1,0) and y-axis (0,2). Directrix of parabola P is : (A) x−2y=0 (B) x+2y=0 (C) 2x−y=0 (D) 2x+y=0
09:58View SolutionGiven A≡(1,1) and AB is any line through it cutting the x-axis at B. If AC is perpendicular to AB and meets the y-axis in C , then the equation of the locus of midpoint P of BC is (a) x+y=1 (b) x+y=2 (c) x+y=2xy (d) 2x+2y=1
06:14View SolutionThe equation of the line that passes through (10,−1) and is perpendicular to y=x24−2 is (a)4x+y=39 (b) 2x+y=19 (c)x+y=9 (d) x+2y=8
02:27View SolutionGiven A≡(1,1) and AB is any line through it cutting the x-axis at B. If AC is perpendicular to AB and meets the y-axis in C , then the equation of the locus of midpoint P of BC is (a) x+y=1 (b) x+y=2 (c) x+y=2xy (d) 2x+2y=1
06:42View Solutionthe line xa−yb=1 cuts the x-axes at P.the equation of the line passes through point P and perpendicular to the line is:
06:29View SolutionLet A be any point on the x-axis and B=(2,3). The perpendicular at A to the line AB meets the y-axis at C. Then the locus of midpoint of segment AC as A moves is given by
03:36View SolutionGiven A-=(1,1) and AB is any line through it cutting the x-axist at B. If AC is perpendicular to AB and meets the y-axis in c, then the equatio of the locus of midpoint P of BC is
05:09View Solution
