If the sum of the distances of a point from two perpendicular lines in
a plane is 1, then its locus is
(a)a square (b) a circle
(c) a straight line (d) two intersecting linesSolution in Bengali
a square
a circle
a straight line
two intersecting lines
The correct Answer is:A
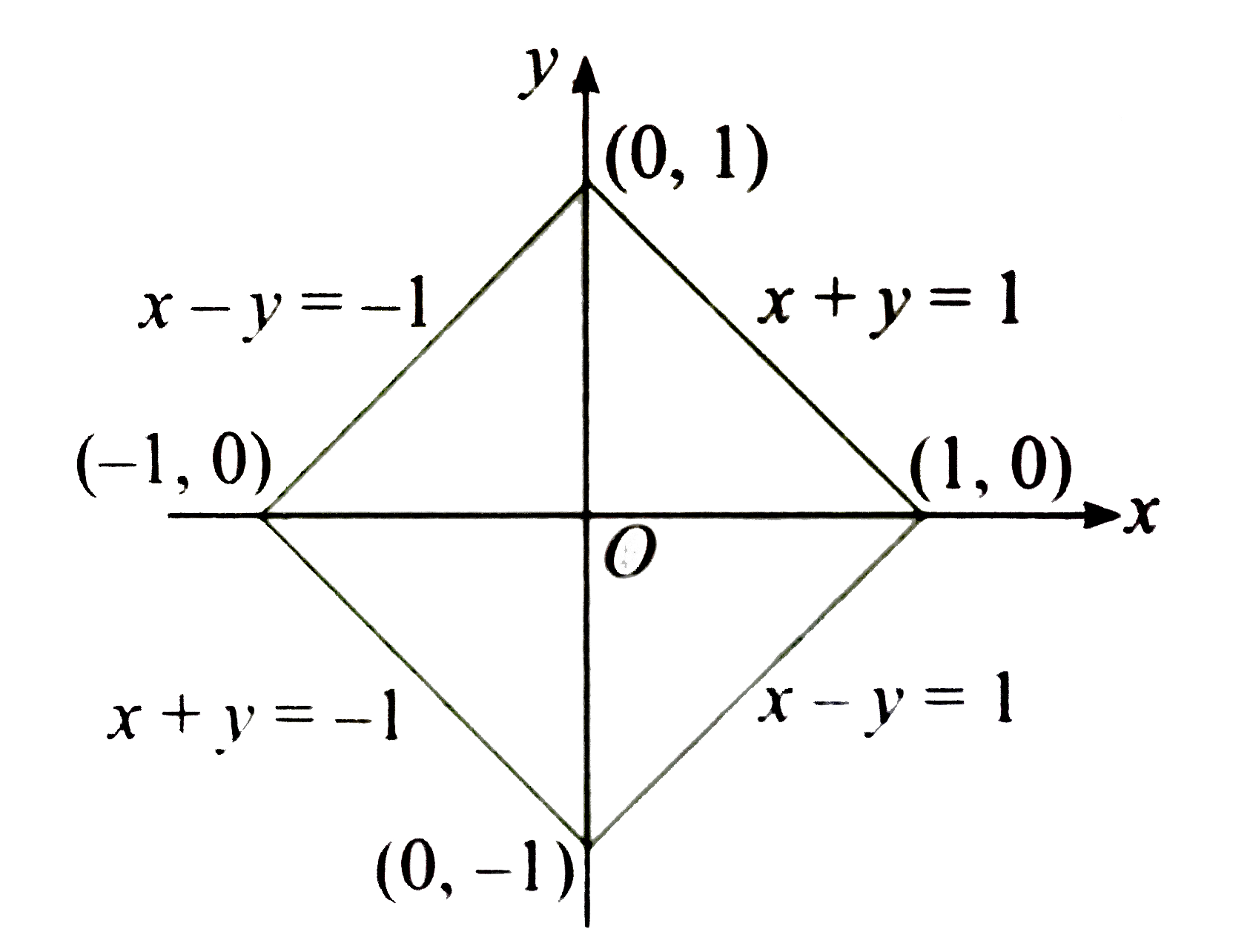
Let the two perpendicular lines be taken as the coordinates axes. If (h,k) is any point on the locus, then according to the given condition, |h|+|k|=1. Hence, the locus of (h,k) is |x|+|y|=1. This consists of four line segments enclosing a square as shown in the figure.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
30 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)
27 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
View SolutionLet l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionIn a plane sum of distances of a point with two mutually perpendicular fixed line is one then locus of the point is - 1.square 2. cirlce 3. two intersecting lines 4. straight line
View SolutionA point moves so that the sum of the squares of its distances from two intersecting straight lines is constant. Prove that its locus is an ellipse.
View SolutionIf the sum of the distances of a point from two perpendicular lines in a plane is 1, then its locus is a square (b) a circle a straight line (d) two intersecting lines
View SolutionA point moves such that the sum of the square of its distances from two fixed straight lines intersecting at antle 2α is a constant. The locus of points is an ellipse os eccentricity
View SolutionAssertion (A): The sum of the distances of a point from two perpendicular lines is 1, then its locus is a square
Reason (R): The locus of a point which is at a distance 'p' from the given point is a circle
View SolutionIf p1,p2 are the perpendicular distance from the origin to the two perpendicular to each other, then the locus of the point of intersection of the perpendicular lines is
View SolutionIf the sum of the distances of a point from two perpendicular lines in a plane is 1, then its locus is(A) a square (b) a circle (C) a straight line (d) two intersecting lines
View SolutionIf the sum of the distances of a point from two perpendicular lines in a plane is 1, then its locus is
(a)a square (b) a circle (c) a straight line (d) two intersecting lines
View SolutionA point moves so that the sum of the squares of its distances from two intersecting straight lines is constant. Prove that its locus is an ellipse.
View Solutionदो परस्पर लम्बवत् सरल रेखाओं पर स्थित एक बिन्दु P से दूरी का योग 1 इकाई है, तब P का बिन्दुपथ है
View Solution
