Question

Let $f:R\to R$ be defined as $f\left(x\right)=e^{\text{sgn}x}+e^{x^2}$. Then find the range of the function, and also indentify the type of the function : one-one or many-one.

Explanation

`f(x) = e^("sgn "x) + e^(x^(2))`
`" "= {{:( (1)/(e)+ e^(x^(2))",",, x lt 0),( 2"," ,, x=0 ),(e+e^(x^(2))",",, x gt 0):}`
For ` x gt 0, x^(2) gt 0, e^(x^(2)) gt1 therefore e^(x^(2)) gt 1 + e`
For `x lt 0, x^(2) gt 0, e^(x^(2)) gt 1 therefore (1)/(e) + e^(x^(2)) gt 1 + (1)/(e)`
Thus the graph of the function is as follows

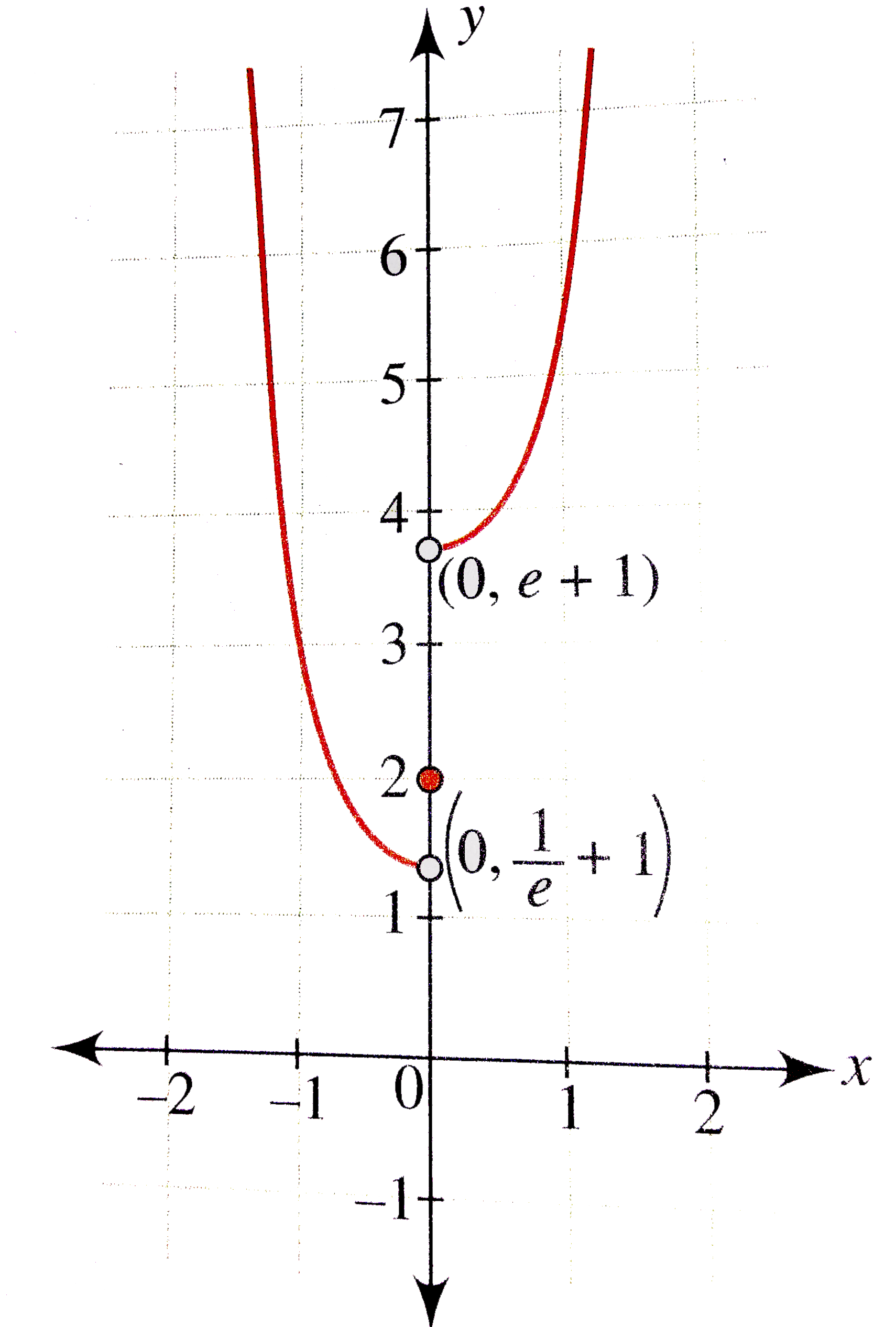
From the graph, the range of the function is `(1+ (1)/(e), oo)`.
Also from the graph, the function is many-one.