Let f:R→R be defined as f(x)=esgn x+ex2. Then find the range of the function, and also indentify the type of the function : one-one or many-one. Solution in Tamil
f(x)=esgn x+ex2
=⎧⎪
⎪⎨⎪
⎪⎩1e+ex2,x<02,x=0e+ex2,x>0
For x>0,x2>0,ex2>1∴ex2>1+e
For x<0,x2>0,ex2>1∴1e+ex2>1+1e
Thus the graph of the function is as follows
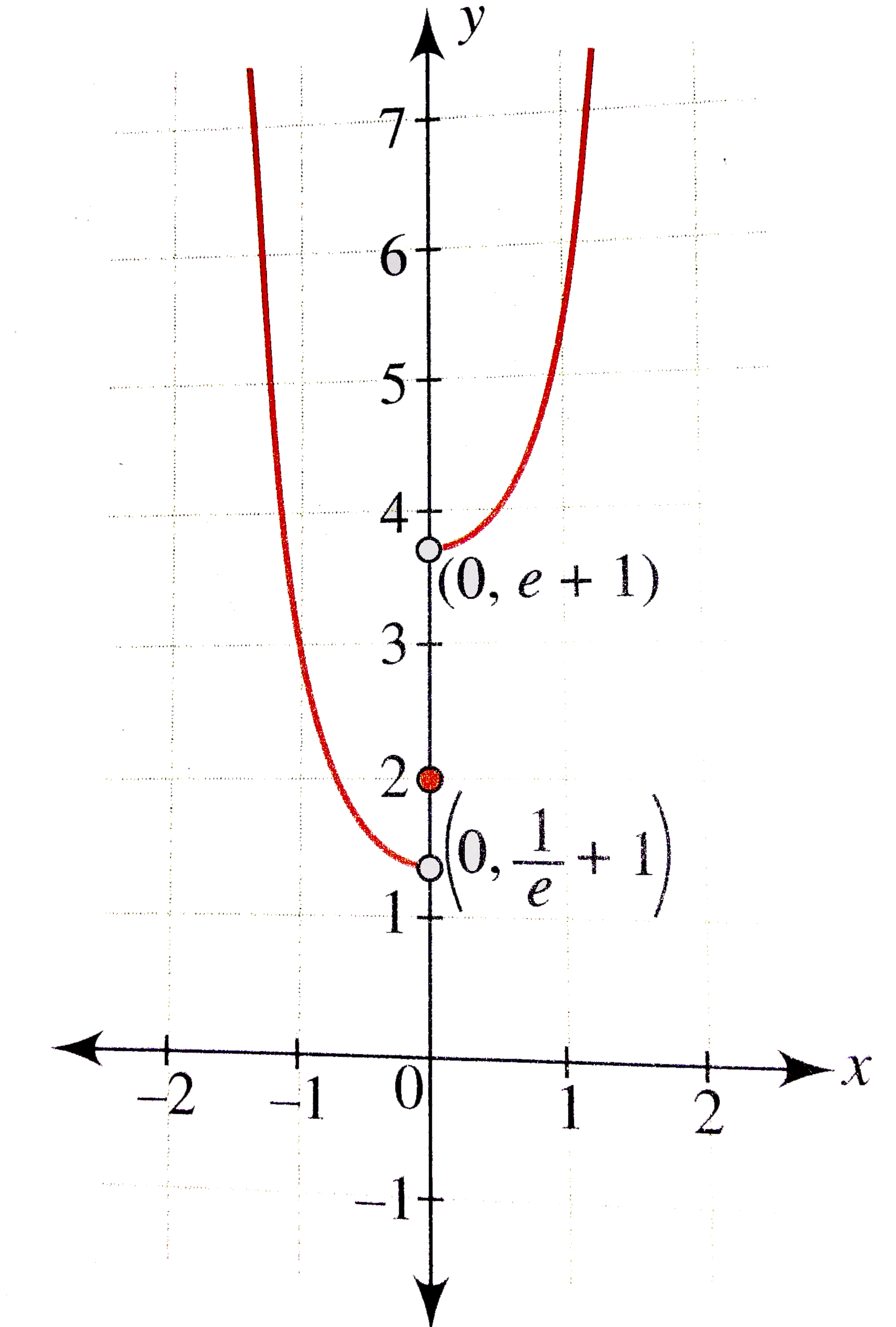
From the graph, the range of the function is (1+1e,∞).
Also from the graph, the function is many-one.
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionLet f:R→R be defined as f(x)=esgn x+ex2. Then find the range of the function, and also indentify the type of the function : one-one or many-one.
View SolutionIf R is the set of real numbers and a function f:R→R is defined as f(x)=x2,x∈R, then prove that f is many-one into function.
View SolutionProve that the function f:R+→R which is defined as f(x)=logex is one - one .
View Solutionफलन f(x)=ex2−e−x2ex2+e−x2 द्वारा परिभाषित फलन f : R→ Rहै----
View SolutionLet f:R+→{−1,0,1} defined by f(x)=sgn(x−x4+x7−x8−1) where sgn denotes signum function then f(x) is (1) many- one and onto (2) many-one and into (3) one-one and onto (4) one- one and into
View SolutionLet f:R→R, be defined as f(x)=ex2+cosx, then is (a) one-one and onto (b) one-one and into (c) many-one and onto (d) many-one and into
View SolutionLet f:R→R be defined as f(x)=esgn x+ex2. Then find the range of the function, and also indentify the type of the function : one-one or many-one.
View SolutionLet f:R→R be defined by f(x)=ex−e−x. Prove that f(x) is invertible. Also find the inverse function.
View Solutionf:R→R is a function defined by f(x)=e|x|−e−xex+e−x. Then f is:
View SolutionProve that the function f:R+→R which is defined as f(x)=logex is one - one .
View SolutionLet f : R^+ ->{-1, 0, 1} defined by f(x) = sgn(x-x^4 + x^7-x^8-1) where sgn denotes signum function then f(x) is (1) many- one and onto (2) many-one and into (3) one-one and onto (4) one- one and into
View SolutionLet f: R-> R , be defined as f(x) = e^(x^2)+ cos x , then is (a) one-one and onto (b) one-one and into (c) many-one and onto (d) many-one and into
View Solution
