Question

Prove that $\sin x+2x\ge \frac{3x(x+1)}{\pi },\forall x\in [0,\frac{\pi }{2}]$ (Justify the inequality, if any used).

Explanation

Let `f(x) = sin x + 2x - (3x(x + 1))/(pi)`
`therefore` `f'(x) = cos x + 2 - (3)/(pi)(2x + 1)`
Let `f'(x) = 0`
`therefore` `cos x = (6)/(pi)x + (3)/(pi) - 2`
Now draw the graphs of y = cos x and `y = (6)/(pi)x + (3)/(pi) - 2` as shown in the following figure.

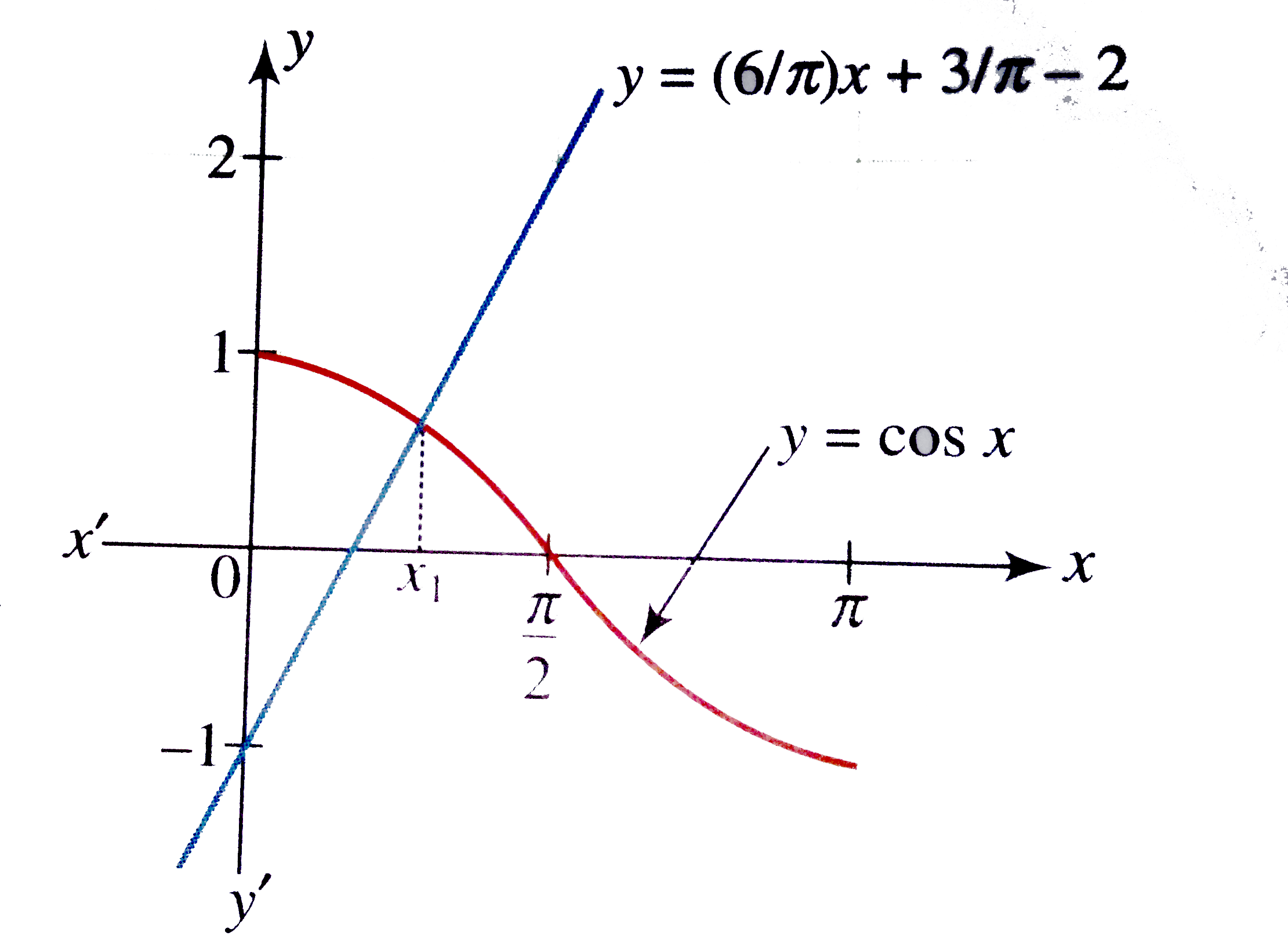
The graphs of y = cos x and `y = (6)/(pi)x + (3)/(pi) - 2` intersect only once.
From the graph, `f'(x) = 0` for some `x = x_(1) in [0, (pi)/(2)]`
For `x lt x_(1)`, the graph of y = cos x lies above the graph of `y = (6)/(pi)x + (3)/(pi) - 2`
For `x gt x_(1)`, the graph of y = cos x lies below the graph of `y = (6)/(pi)x + (3)/(pi) - 2`
Thus, `f'(x) gt 0 " for " x lt x_(1)`, where f(x) increases, and `f'(x) lt 0` for `x gt x_(1)`, Where f(x) decreases.
Also `f''(x) = -sin x - (3)/(pi)(2) lt 0`, so the graph is concave downwards.
So `x = x_(1)` is the point of maxima.
`f(0) = 0, f((pi)/(2)) = (pi)/(4) - (1)/(2)`
Graph of y = f(x) is as shown in the following figure.

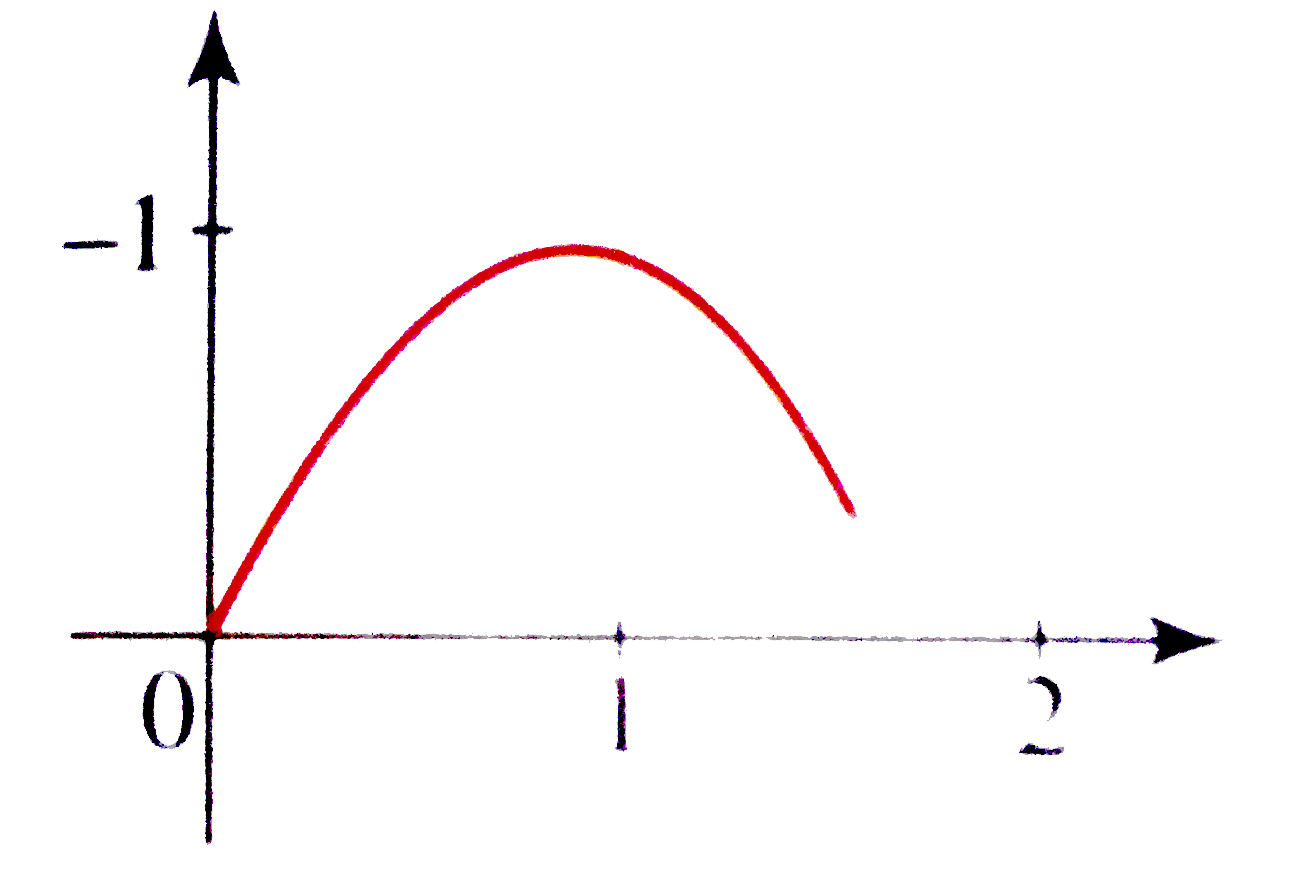
The graph lies completely above the x - axis, so `f(x) gt 0.`