Let f(x)=xsinπx, x>0 . Then for all natural numbers n, f′(x) vanishes at (a) A unique point in the interval (n, n+12) (b) a unique point in the interval (n+12, n+1) (c) a unique point in the interval (n, n+1) (d) two points in the interval (n, n+1)Solution in Bengali
We have f'(x)=sinπx+πxcosπx=0
⇒ tanπx=−πx
Now we draw the graphs of y=tanπx and y=−πx and look for their points of intersection. y=tanπx has period 1.
Graphs are as shown in the following figure.
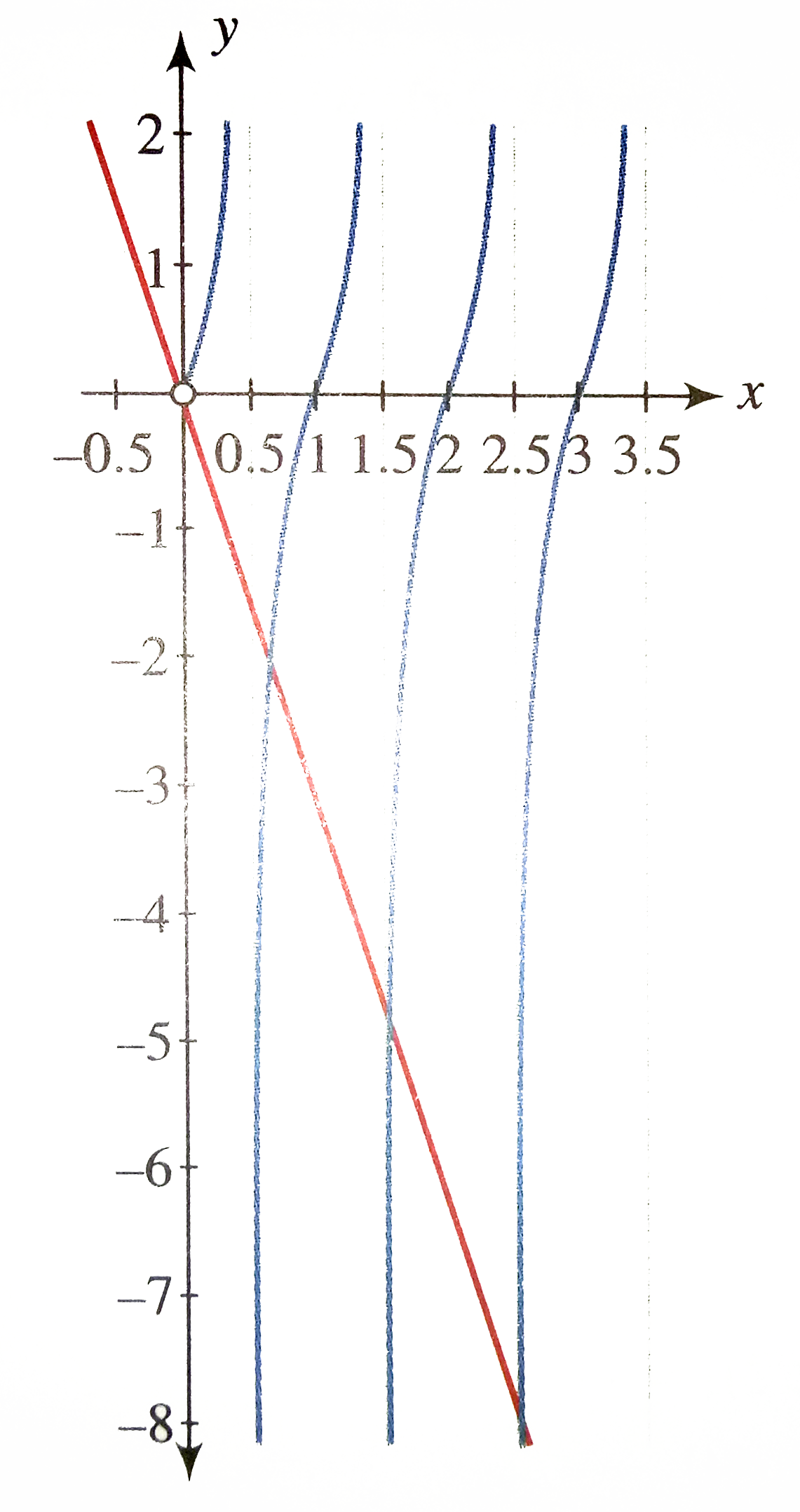
⇒ x∈(n+12,n+1)or(n,n+1)
Hence (b) and (c) are correct options.
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
Similar Questions
Draw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionDraw the graph of y=1(1/x).
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionLet f(n)=1+12+13++1n. Then f(1)+f(2)+f(3)++f(n) is equal to
(a)nf(n)−1
(b) (n+1)f(n)−n
(c)(n+1)f(n)+n
(d) nf(n)+n
View SolutionLet f(x)=xsinπx,x>0. Then for all natural numbers n,f′(x) vanishes at (A)a unique point in the interval (n,n+12) (B)a unique point in the interval (n+12,n+1) (C)a unique point in the interval (n,n+1) (D)two points in the interval (n,n+1)
View SolutionIf int(dx)/(x^(2)(x^(n)+1)^((n-1)/(n)))=-(f(x))^((1)/(n))+C then f(x) is (A)1+x^(n)(B)1+x^(-n)(C)x^(n)+x^(-n)(D)x^(n)-x^(-n)
View Solutionf(x)=(x+x^(2)+......+x^(n)-n)/(x-1),x!=1 then value of f(1) so that f is continuous is (A) n(B)(n(n-1))/(2) (C) (n(n+1))/(2) (D) (n+1)/(2)
View SolutionSuppose the function f(x)=xn,n≠0 is differentiable for all x. Then n can be any element of the interval
View Solutionयदि a0n+1+a1n+a2n−1+...+an−12+an=0 तब सिद्ध कीजिए की अंतराल [0,1] में एक ऐसे x का अस्तित्व होगा जिसके लिए a0xn+a1xn−1+...+an=0
View SolutionIf f(x)=1+xm(x−1)n,m,n∈N, then f'(x)=0 has atleast one root in the interval
View SolutionLet f(n)=1+12+13++1n. Then f(1)+f(2)+f(3)++f(n) is equal to
(a)nf(n)−1
(b) (n+1)f(n)−n
(c)(n+1)f(n)+n
(d) nf(n)+n
View SolutionLet f(x)=xsinπx,x>0. Then for all natural numbers n,f′(x) vanishes at (A)a unique point in the interval (n,n+12) (B)a unique point in the interval (n+12,n+1) (C)a unique point in the interval (n,n+1) (D)two points in the interval (n,n+1)
View SolutionLet f(x)=xsinπx, x>0 . Then for all natural numbers n, f′(x) vanishes at (a) A unique point in the interval (n, n+12) (b) a unique point in the interval (n+12, n+1) (c) a unique point in the interval (n, n+1) (d) two points in the interval (n, n+1)
View SolutionIf ∫dxx2(xn+1)n−1n=−(f(x))1n+C then f(x) is (A) 1+xn (B) 1+x−n (C) xn+x−n (D) xn−x−n
View Solutionf(x) एक सतत् फलन है, जो एक संवृत्त अन्तराल [a,b] पर परिभाषित है, तब limn→∞n−1∑r=01nf(rn)=∫10f(x)dx
limn→∞1n{1n+1+2n+2+...+3n4n} का मान होगा
View SolutionLet f(x) be a continous function defined on the closed interval [a,b] then limn→∞∑n1nr=1f(rn)=∫10f(x)dx
The value of limn→∞(1n)[(1n+1)+2n+2+......+12} is
View Solution
