Eight players P1,P2,P3,...........P8, play a knock out tournament. It is known that whenever the players PiandPj, play, the player Pi will win if i<j. Assuming that the players are paired at random in each round, what is the probability that the players P4, reaches the final ?Solution in Bengali
P1P2P3P4P5P6P7P8
Given that if Pi,Pj play with i<j, then Pi will win. For the first round, P4 should be paired with any one from P5 to P8. It can be done in .4C1 ways. Then P4 to be the finalist, at least one player from P5 to P8 should reach in the second round. Therefore, one pair should be from remaining 3 from P5 to P8 in .3C2. Then round, we have four players. Favorable ways is 1.
Now, total possible pairings is
.8C2×.6C2×.4C2×.2C24!×.4C2×.2C22!
Therefore, the probability is
.4C1.3C2.3C24!2!.8C2.6C2.4C2.2C2.4C2.2C2=435
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.1
6 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.2
19 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - JEE Advanced
7 Videos
- PROBABILITYBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITYEXERCISE - All Questions
470 Videos
- PROBABILITY IIBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
Similar Questions
Which of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
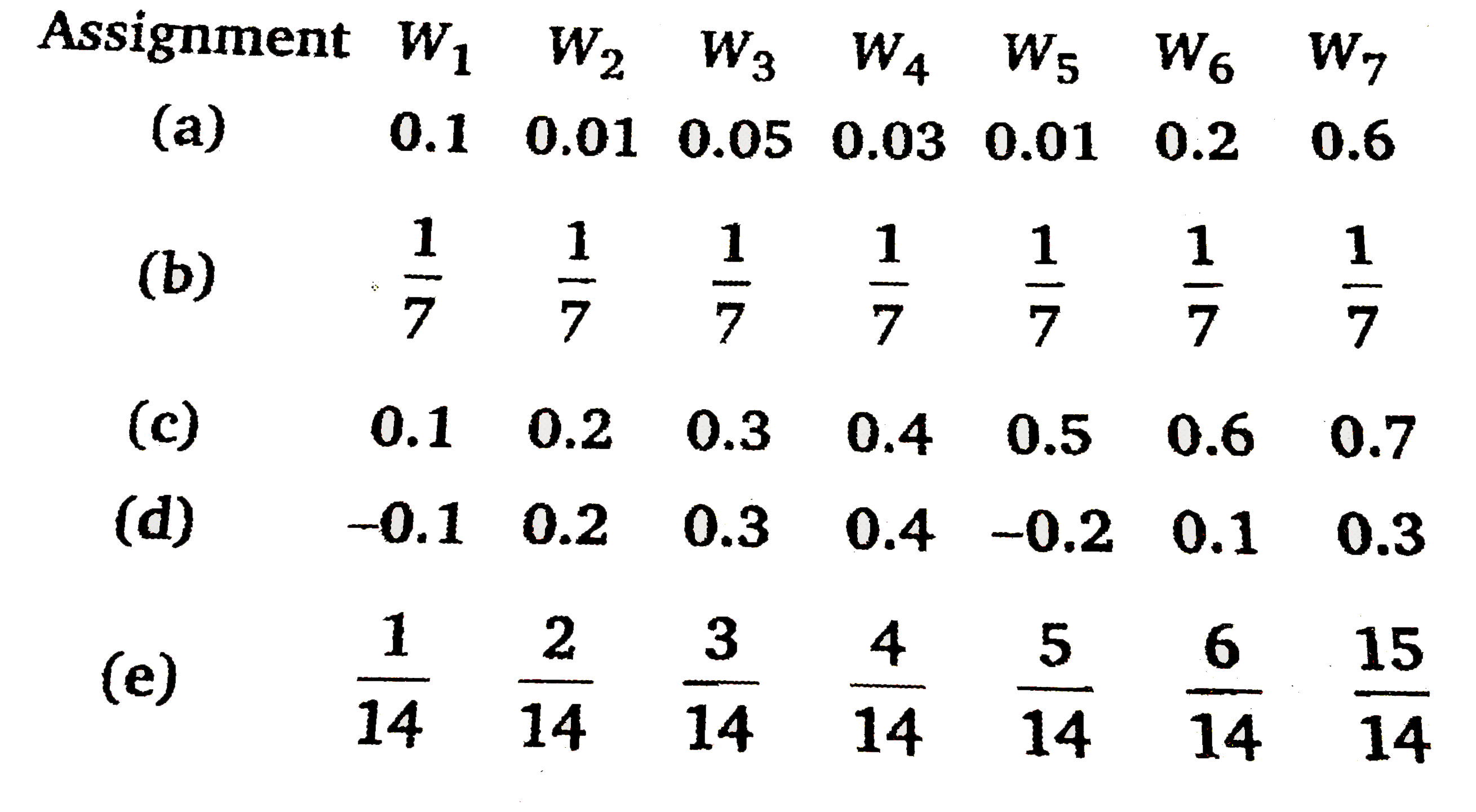
View SolutionIf two fair dices are thrown and digits on dices are a and b, then find the probability for which ωab=1, (where ω is a cube root of unity).
View SolutionLet ω be a complex cube root unity with ω≠1. A fair die is thrown three times. If r1,r2andr3 are the numbers obtained on the die, then the probability that ωr1+ωr2+ωr3=0 is 1/18 b. 1/9 c. 2/9 d. 1/36
View SolutionA coin is tossed three times, consider the following events. A : ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two appear’. Do they form a set of mutually exclusive and exhaustive events?
View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
View SolutionEight players P1,P2,P3,...........P8, play a knock out tournament. It is known that whenever the players PiandPj, play, the player Pi will win if i<j. Assuming that the players are paired at random in each round, what is the probability that the players P4, reaches the final ?
View SolutionSixteen players S1,S2,…,S16 play in a tournament. They are divided into eight pairs at random. From each pair a winner is decided on the basis of a game played between the two players decided to the basis of a game played between the two players of the pair. Assume that all the players are of equal strength.
(a) Find the prabability that the player S1 is among the eight winners.
(b) Find the probability that exactly one of the two players S1andS2 is among the eight winners.
View SolutionIn a badminton each player played one game with ll the other players. Number of players participated in the tournament if they played 105 games is
View Solution8 players P1,P2,P3,…,P8 play a knock out tournament. It is known that all the players are of equal strength. The tournament is held in three rounds where the players are paired at random in each round. If it is given that P1 wins in the third round. If p be the probability that P2 loses in second round, then the value of 7p is
View SolutionEight players P1,P2,P3,...........P8, play a knock out tournament. It is known that whenever the players PiandPj, play, the player Pi will win if i<j. Assuming that the players are paired at random in each round, what is the probability that the players P4, reaches the final ?
View Solutionआठ खिलाड़ी P1,P2,P3,………….P8 एक नॉक आऊट टूर्नामेंट खेलते है। यह ज्ञात है कि जब Pi तथा Pj खिलाड़ी खेलते है तो Pi खिलाड़ी जीतता है यदि i<j है। माना प्रत्येक पारी में खिलाड़ियों के यादृच्छया युग्म बनाते है तो खिलाड़ी P4 के फाइनल में पहुचने की प्रायिकता क्या है?
View Solutionचार खिलाड़ियों P1,P2,P3,P4, में से तीन खिलाड़ियोंं की टीम बनाने के तरीकों की संख्या बताओ ।
View Solution16 players P_1,P_2, P_3,........P_(16) , Participate in a tennis competition. The player with the lower attachment plays better than the player with the higher attachment. These players are divided into 4 groups and there are 4 players in each group and the players who play well in each group are selected for the semi-finals. If P_1,P_2, P_3, And P_4 If the players are in different groups, then there will be number of ways to divide the players into 4 equal groups.
View Solution16 players P_1,P_2, P_3,........P_(16) , Participate in a tennis competition. The player with the lower attachment plays better than the player with the higher attachment. These players are divided into 4 groups and there are 4 players in each group and the players who play well in each group are selected for the semi-finals. If a player who plays well from each group is selected ( P_6 One of them is) then the number of ways to divide 16 players into four equal groups (k) (12!)/((4!)^3) Is, then the value of k is
View SolutionIn a badminton tournament each player played one game with all the other players. How many players participated in the touinament if they played 105 games in all?
View SolutionIn a badminton each player played one game with ll the other players. Number of players participated in the tournament if they played 105 games is
View Solution
