Let P(x) denote the probability of the occurrence of event x. Plot all those point (x,y)=(P(A),P(B)) in a plane which satisfies the conditions, P(A∪B)≥3/4and1/8≤P(A∩B)≤3/8Solution in Bengali
P(A∪B)≥34and18≤P(A∩B)≤38
Hence,
P(A)+P(B)−P(A∩B)≤34
implies P(A)+P(B)≥34+P(A∩B)≥34+18=78
⇒x+y≥78
We know that
P(A∩B)≤1
⇒P(A)+P(B)≤1+P(A∩B)≤1+38=118
⇒x+y≤118
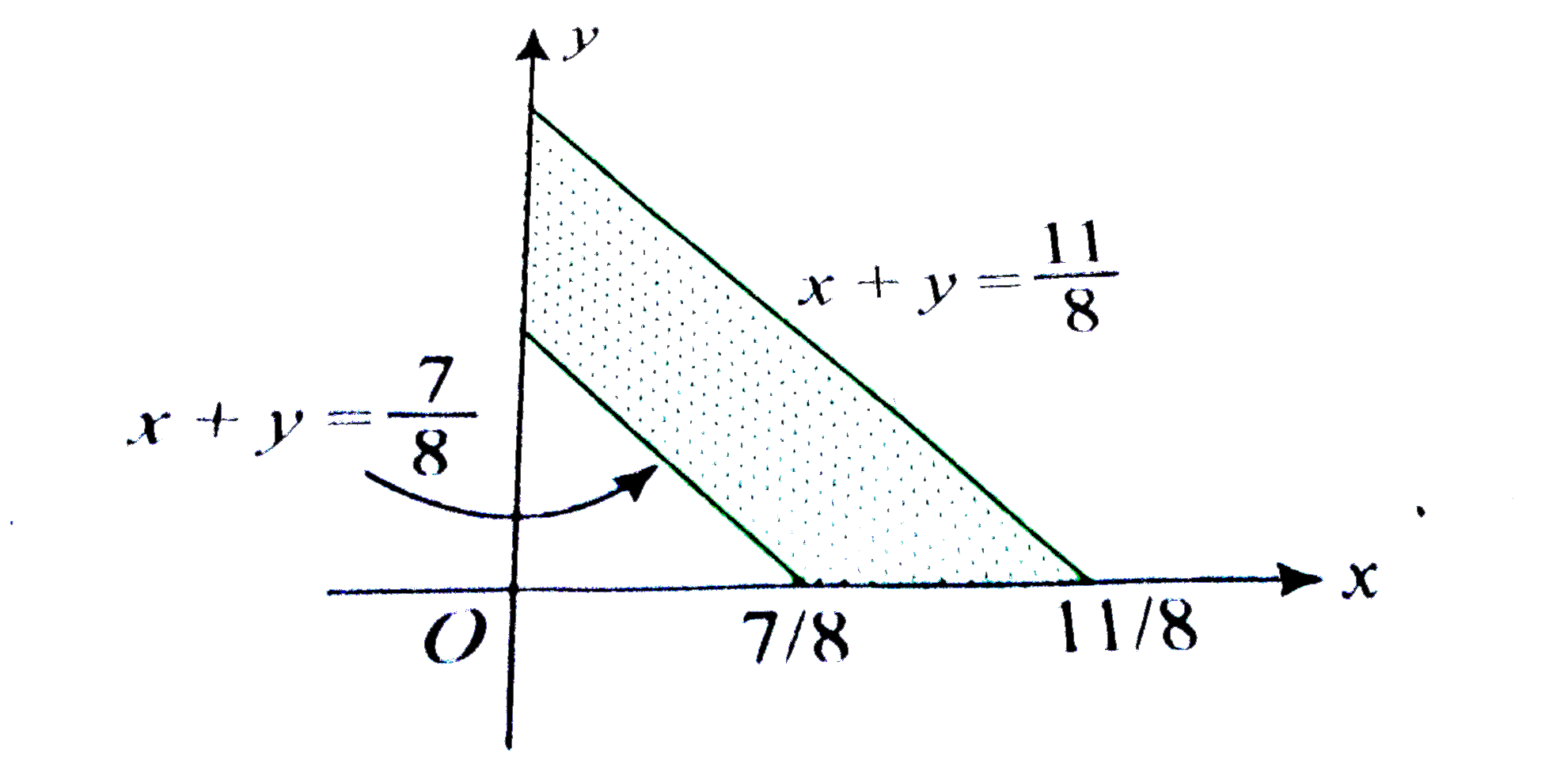
The shaded part in the figure is the required region.
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.1
6 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.2
19 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - JEE Advanced
7 Videos
- PROBABILITYBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITYEXERCISE - All Questions
470 Videos
- PROBABILITY IIBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
Similar Questions
Which of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
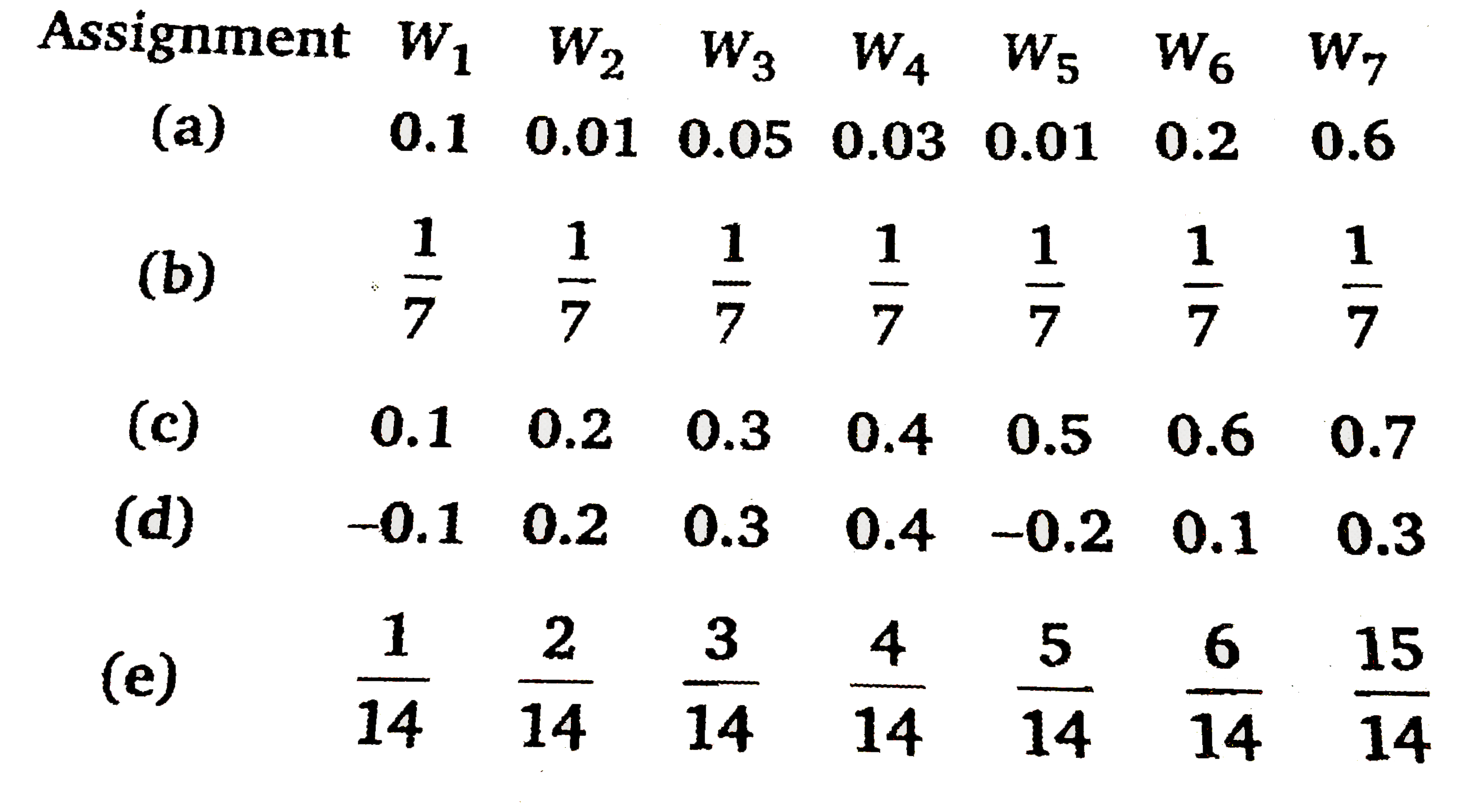
View SolutionIf two fair dices are thrown and digits on dices are a and b, then find the probability for which ωab=1, (where ω is a cube root of unity).
View SolutionLet ω be a complex cube root unity with ω≠1. A fair die is thrown three times. If r1,r2andr3 are the numbers obtained on the die, then the probability that ωr1+ωr2+ωr3=0 is 1/18 b. 1/9 c. 2/9 d. 1/36
View SolutionA coin is tossed three times, consider the following events. A : ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two appear’. Do they form a set of mutually exclusive and exhaustive events?
View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
View SolutionFor a point P in the plane, let d1 (P) and d2 (P) be the distance of the point P from the lines x – y = 0 and x + y = 0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2 < d1(P) + d2 (P)< 4, is
View SolutionLet P(x) denote the probability of the occurrence of event x. Plot all those point (x,y)=(P(A),P(B)) in a plane which satisfies the conditions, P(A∪B)≥3/4and1/8≤P(A∩B)≤3/8
View SolutionLet AandB be two event such that P(A∪B)≥3/4 and 1/8≤P(A∩B)≤3/8. Statement 1: P(A)+P(B)≥7/8. Statement 2:P(A)+P(B)≤11/8.
View SolutionIf A is an event and P(A) and P(vec A) denote the probabilities of occurrence and non occurrence respectively of event A, the P(A)+P(vec A)
View SolutionLet P(x) denote the probability of the occurrence of event x. Plot all those point (x y) = (P(A), P(B)) in a plane which satisfy the conditions, P(A∪B)≥3/4and1/8≤P(A∩B)≤3/8
View Solutionमाना कि A और B दो घटनाएँ है तथा P(A)=0.3P(B)=0.4,P(A∪B)=0.5 तो P(A∩B) है।
View SolutionP(A∪B)=P(A)−P(B)+P(A∩B)
View SolutionIf A and B are any two events such that P(A)=25 and P(A∩B)=320, then the conditional probability, P(A/(A'∪B')), where A' denotes the complement of A, is equal to
View SolutionIf A and B are two events such that P(A∪B)=56, P(A∩B)=13 and P(A)=23 then A and B are
View SolutionLet P(x) denote the probability of the occurrence of event x. Plot all those point (x,y)=(P(A),P(B)) in a plane which satisfies the conditions, P(A∪B)≥3/4and1/8≤P(A∩B)≤3/8
View SolutionLet AandB be two event such that P(A∪B)≥3/4 and 1/8≤P(A∩B)≤3/8. Statement 1: P(A)+P(B)≥7/8. Statement 2:P(A)+P(B)≤11/8.
View Solution
