A box contains two 50 paise coins, five 25 paise coins and a certain fixed number N(≥2) of 10 and 5-paise coins. Five coins are taken out of the box at random. Find the probability that the total value of these 5 coins is less than 1 rupee and 50 paise.Solution in Bengali
Here the total number of coins is N + 7, Therefore, the total number of ways of choosing 5 coins out of N + 7 is .n+7C5.
Let E denote the event that the sum of the values of the coins is less than 1 rupee and 50 paise. Then E' denotes the event that the total values of the five coins is equal to or more than 1 rupee and 50 paise. The number of cases favourable to E' is
.2C1×.5C4×.NC0+.2C2×.5C3×.NC0+.2C2×.5C2×.NC1=2×5+10+10N=10(N+2)
∴P(E')=10(N+2).N+7C5
⇒P(E)=1−P(E')=1−10(N+2).N+7C5
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.1
6 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.2
19 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - JEE Advanced
7 Videos
- PROBABILITYBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITYEXERCISE - All Questions
470 Videos
- PROBABILITY IIBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
Similar Questions
Which of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
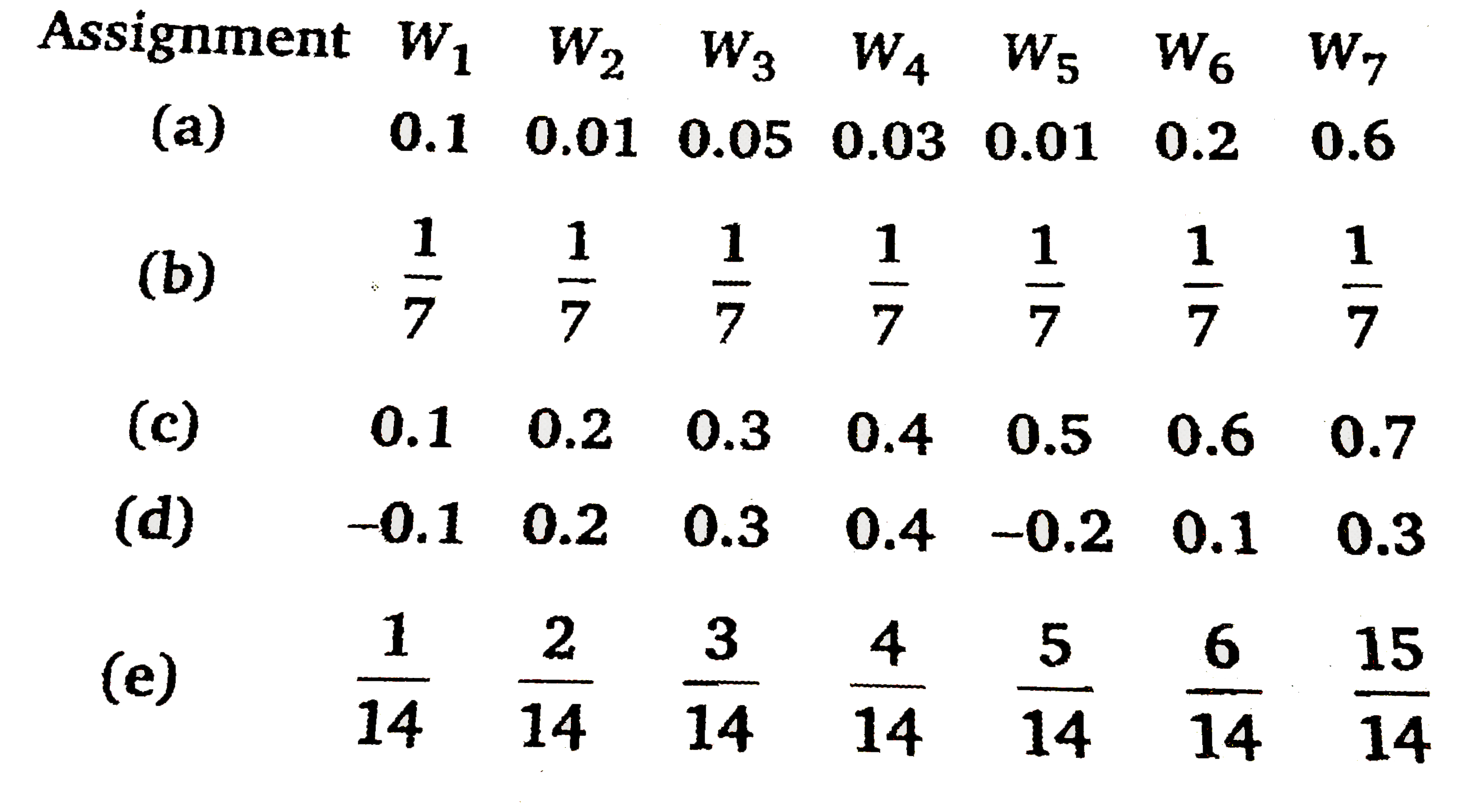
View SolutionIf two fair dices are thrown and digits on dices are a and b, then find the probability for which ωab=1, (where ω is a cube root of unity).
View SolutionLet ω be a complex cube root unity with ω≠1. A fair die is thrown three times. If r1,r2andr3 are the numbers obtained on the die, then the probability that ωr1+ωr2+ωr3=0 is 1/18 b. 1/9 c. 2/9 d. 1/36
View SolutionA coin is tossed three times, consider the following events. A : ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two appear’. Do they form a set of mutually exclusive and exhaustive events?
View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
View SolutionA box contains two 50 paise coins, five 25 paise coins and a certain fixed number N(≥2) of 10 and 5-paise coins. Five coins are taken out of the box at random. Find the probability that the total value of these 5 coins is less than 1 rupee and 50 paise.
View SolutionA bag contains 25 paise and 50 paise coins whose total value is Rs 30. If the number of 25 paise coins is four times that of 50 paise coins, find the number of each type of coins.
View Solutionएक बक्से में रू 180 है जो कि एक रू 50 पैसे और 25 पैसे को सिक्के के सिक्को कि संख्या का अनुपात 2:3:4 है ! 50 पैसे के सिक्को
View SolutionA bag contains one rupee, 50 paise and 25 paise coins. The ratio of the number of 1 rupee coins to that of 50 paise coins is 5:9 and the ratio of the number of 50 paise conins to that of 25 paise coins is 2:1 . Find the value of the 50 paise coins in the bag if the total value of the bag is Rs. 425.
View SolutionA box contains 2 fifty paise coins, 5 twenty five paise coins and a certain fixed number n(≥2) of ten and five paise coins. Five coins are taken out of the box at random. Find the probability that the total value of these 5 coins is less than one rupee and fifty paise.
View Solution5. The amount of ₹ 90 in a bag is 50 paise, 25 paise and 10 paise, in the form of coins. If 50 paise, 25 paise and 10 paise coins are in the ratio 2: 3: 5, then number of 25 paise coins in the bag is
View Solutionएक बक्से में दो 50 पैसे के सिक्के, पांच 25 के सिक्के और निश्चित संख्या N(≥2) में 10 और 5 पैसे के सिक्के हैं। बक्से में से पांच सिक्के यदृच्छया निकाले जाते हैं। 5 सिक्कों का कुल मान एक रूपये पचास पैसे से कम होने की प्रायिकता ज्ञात कीजिए।
View SolutionRs180 contained in a box of one rupee, 50 paise and 25 paise coins in the ratio 2:3:4. What is the number of 50 paise coins?
View SolutionA box contains two 50 paise coins, five 25 paise coins and a certain fixed number N(≥2) of 10 and 5-paise coins. Five coins are taken out of the box at random. Find the probability that the total value of these 5 coins is less than 1 rupee and 50 paise.
View SolutionA bag contains 25 paise and 50 paise coins whose total value is Rs30. If the number of 25 paise coins is four times that of 50 paise coins, find the number of each type of coins.
View Solution25 पैसे के सिक्के, 10 पैसे के सिक्के तथा 50 पैसे के सिक्के में दिए गए । 10 पैसे के सिक्कों की संख्या 25 पैसे के सिक्कों की संख्या 4 गुनी थी और 50 पैसे के सिक्कों की संख्या की 10 पेसै के सिक्कों की संख्या की दुगुनी है । प्रत्येक प्रकार के सिक्कों की संख्या ज्ञात कीजिए।
View Solution
