Prove that each of the following diagonals of a parallelogram divides it into two congurent triangles. The following lowing are the steps involved in proving the above results. Arrange them in sequential order.
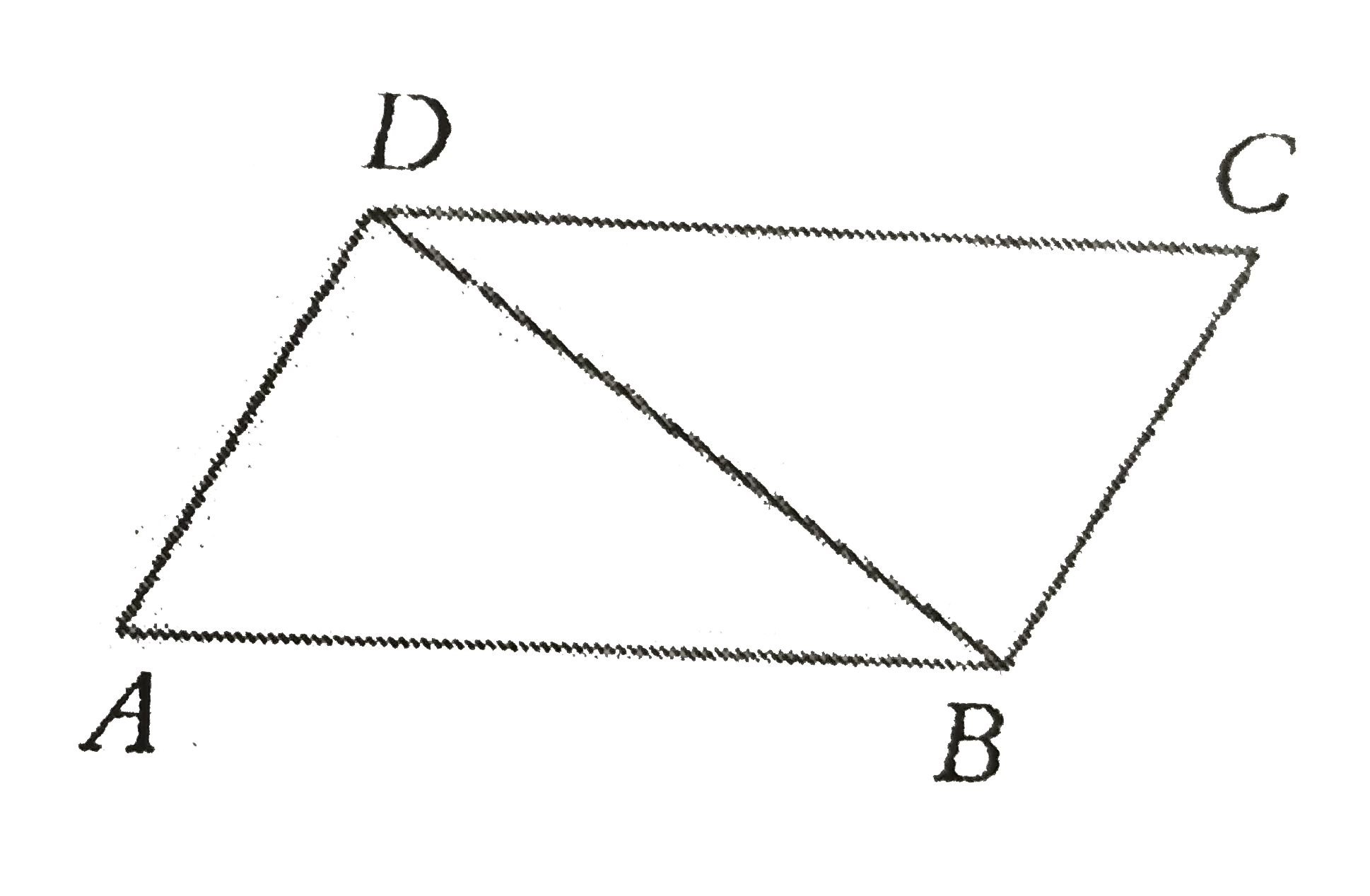
(A) By SSS conguruence property , .
(B) Let ABCD be a parallelogram and join BD.
(C ) (opposite sides of parallelogram) and (common side).
(D ) Similarly , AC divides the parallelogram into two congruent triangles.
ABCD
BCAD
BACD
CBAD
The correct Answer is:B
Step by step video, text & image solution for Prove that each of the following diagonals of a parallelogram divides it into two congurent triangles. The following lowing are the steps involved in proving the above results. Arrange them in sequential order. (A) By SSS conguruence property , Delta DAB ~= Delta BCD. (B) Let ABCD be a parallelogram and join BD. (C ) AB=CD,AD=BC(opposite sides of parallelogram) and BD =BD (common side). (D ) Similarly , AC divides the parallelogram into two congruent triangles. by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRY Book:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRY Exercise:TEST YOUR CONCEPTS (ESSAY TYPE QUESTIONS)
Explore 5 Videos
- FormulaeBook:PEARSON IIT JEE FOUNDATIONChapter:FormulaeExercise:Level 3
Explore 7 Videos
- INDICESBook:PEARSON IIT JEE FOUNDATIONChapter:INDICESExercise:CONCEPT APPLICATION (Level 3)
Explore 7 Videos
Similar Questions
Prove that each of the following diagonals of a parallelogram divides it into two congurent triangles. The following lowing are the steps involved in proving the above results. Arrange them in sequential order.

(A) By SSS conguruence property , ΔDAB≅ΔBCD.
(B) Let ABCD be a parallelogram and join BD.
(C ) AB=CD,AD=BC(opposite sides of parallelogram) and BD=BD (common side).
(D ) Similarly , AC divides the parallelogram into two congruent triangles.
View SolutionThe diagonal AC of a quadrilateral ABCD divides it into two triangles of equal areas. Prove that diagonal AC bisects the diagonal BD.
View Solution
Knowledge Check
Prove that each of the following diagonals of a parallelogram divides it into two congurent triangles. The following lowing are the steps involved in proving the above results. Arrange them in sequential order.

(A) By SSS conguruence property , ΔDAB≅ΔBCD.
(B) Let ABCD be a parallelogram and join BD.
(C ) AB=CD,AD=BC(opposite sides of parallelogram) and BD=BD (common side).
(D ) Similarly , AC divides the parallelogram into two congruent triangles.AABCDBBCADCBACDDCBADShow that each diagonal of a parallelogram divide it into two congruent triangles.
The following are the steps involved in showing the above result. Arrange them in sequential order.
A) In △ABC and △CDA, AB=DC and BC=AD (∴ opposite angles of parallelogram) AC=AC (common side).
B) Let ABCD be a parallelogram. Join AC.
C) By SSS congruence property, △ABC≅△CDA.
D) Similarly, BD divides the triangle into two congruent triangles.ABACDBBDACCBADCDBDCA
diagonal of a cocyclic parallelogram ABCD is AC and BD intersection at point R. then
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at EandF . Prove that EBFD is a parallelogram.
View SolutionABCD and APCR are the two parallelograms and AC is the common diagonal. Prove that PBRD is a parallelogram.
View SolutionP is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△APD) = ar(△CPD).
View SolutionIn the figure ABCD and DXBY are two parallelograms with BD as the common diagonal. Prove that AYCX is also a parallelogram.
View SolutionThe diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC . Prove that DFxEF=FBxFA.
View Solution