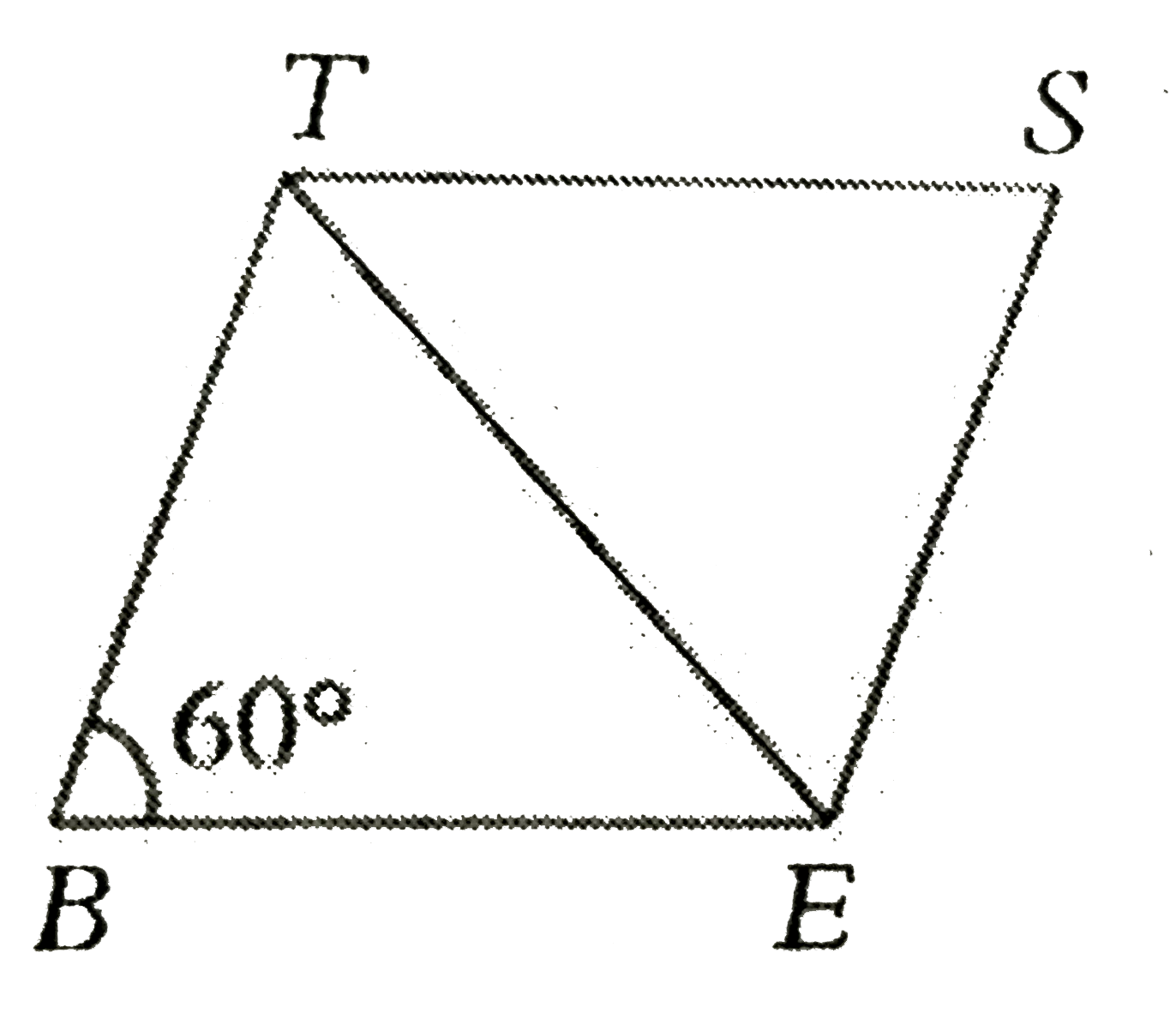
In a rhombus BEST,if ∠B=60∘ and BT=6cm, then find the length of the diagonal TE.
The following are the steps involved in solving the above problem. Arrange them in sequential order.
(A) ⇒Δ BTE is an equilateral triangle.
(B) Join T and E
(C ) In ΔBET,BT=BE⇒∠BTE=∠BET=180∘−60∘2=60∘(∵∠B=60∘) .
(D) TE=6cm
BCAD
BCDA
BACD
BADC
The correct Answer is:A
Step by step video, text & image solution for In a rhombus BEST,if /_ B=60^(@) and BT =6cm, then find the length of the diagonal TE. The following are the steps involved in solving the above problem. Arrange them in sequential order. (A) implies Delta BTE is an equilateral triangle. (B) Join T and E (C ) In Delta BET, BT=BE implies /_ BTE =/_ BET =(180^(@)-60^(@))/(2)=60^(@) ( :' /_ B=60^(@)) . (D) TE=6 cm by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - TEST YOUR CONCEPTS (ESSAY TYPE QUESTIONS)
5 Videos
- FormulaeBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 3
7 Videos
- INDICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)
7 Videos
Similar Questions
Knowledge Check

In a rhombus BEST,if ∠B=60∘ and BT=6cm, then find the length of the diagonal TE.
The following are the steps involved in solving the above problem. Arrange them in sequential order.
(A) ⇒Δ BTE is an equilateral triangle.
(B) Join T and E
(C ) In ΔBET,BT=BE⇒∠BTE=∠BET=180∘−60∘2=60∘(∵∠B=60∘) .
(D) TE=6cmABCADBBCDACBACDDBADCIf 169 =b2+25 then find the value of b .The following sentences are the steps involved in solving the above problem .Arrange them in sequential order from the first to the last
ABACBBCACCABDACBIf tan(A+B)=1andA(−B)=1√2, then find A and B.
The following are the steps involved in solving the above problem. Arrange them in sequential order.
(A) tan(A+B)=1⇒tan(A+B)=tan45∘andsin(A−B)=1√2⇒sin(A−B)=sin45∘.
(B) 2A=90∘⇒A=45∘.
(C ) A+B=45∘andA−B=45∘.
(D) ∴A=45∘andB=0∘.ADBCABCABDCACDBDACBD
Prove that each angle of an equilateral triangle is 600
View SolutionThe perimeter of an equilateral triangle is 60m. The area is
View SolutionIf n(A)=6 and n(B)=8 and n(A∩B)=4, then find n(AΔB).
The following are the step involved in solving the above problem . Arrange them in sequnential order.
(a) n(A∪B)=n(A)+n(B)−n(A∩B)
(b) n(A∪B)=10
(c )n(A∪B)=6+8−4
(d) n(AΔB)=10−4=6
(e) n(AΔB)=n(A∪B)−n(A∩B).
View SolutionThe perimeter of an equilateral triangle is 60m. The area is
View SolutionIf cos(A−B)=12andsin(A+B)=√32, then find A and B
The following are the steps involved in solving the following problem. Arrange them in sequential order.
(A)2A=120∘⇒A=60∘
(B) ∴A=60∘,B=0∘.
(C ) cos(A−B)=12⇒cos(A−B)=cos60∘andsin(A+B)=√32⇒sin(A+B)=sin60∘.
(D)A+B=60∘andA−B=60∘.
View Solution
