ABCD is a kite in which AB=AD and CB=CD. If ∠ABD=30∘and∠BDC=40∘, then find ∠A+∠C.
Video Solution
Text Solution
The correct Answer is:220∘
|
Answer
Step by step video, text & image solution for ABCD is a kite in which AB=AD and CB=CD. If angleABD=30^(@) and angleBDC=40^(@), then find angleA+angleC. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In the given figreu AB∣∣CD,∠BAD=30∘and∠ECD=50∘, find ∠CED
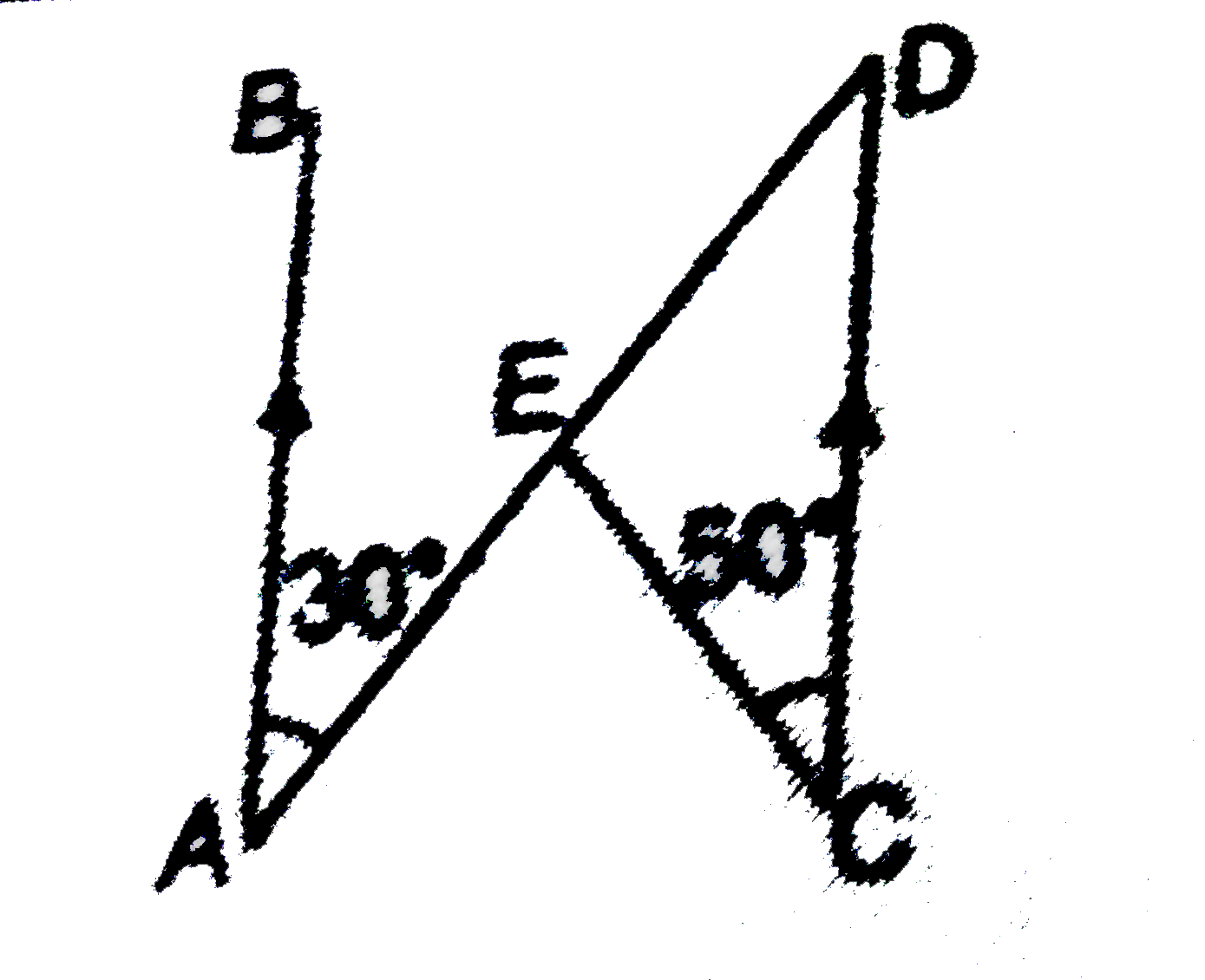 A120∘B30∘C100∘D50∘
A120∘B30∘C100∘D50∘ABCD is a kite in which AB=AD and BC= DC.
The kite is symmetrical about
 Athe diagonal ACBthe diagonal BDCnone of theseDboth (a) and (d)
Athe diagonal ACBthe diagonal BDCnone of theseDboth (a) and (d)ABCD is a cyclic quadrilateral in which AB is a diameter, BC = CD and ∠A=50∘ then ∠DBC is :
A25∘B20∘C45∘D30∘
ABCD is a kite in which AB=AD and CB=CD. If ∠ABD=25∘and∠BDC=35∘, then find ∠A−∠C.
View SolutionIn parallelogram ABCD, if ∠A=(7x+40)∘ and ∠C=(2x+80)∘ , then find ∠A .
View SolutionABCD is a kite in which AB=AD and BC= DC.
The kite is symmetrical about

View SolutionABCD is a quadrilateral in which AB||DC and AD = BC. Prove that ∠A=∠Band∠C=∠D.
View SolutionIn △ABC,AB=10cm,∠A=45∘ and ∠C=60∘. Find BC.
View Solution
