Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by (E2−E1)ˆn=σε0 where ˆn is a unit vector normal to the surface at a point and is the surface charge density at that point. (The direction ofˆn is from side 1 to side 2.) Hence show that just outside a conductor, the electric field isσˆn/ε0Solution in Punjabi
Step by step video solution for Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by (E_2 - E_1) hatn= (sigma)/(epsilon_0) where hatn is a unit vector normal to the surface at a point and is the surface charge density at that point. (The direction ofhat n is from side 1 to side 2.) Hence show that just outside a conductor, the electric field issigma hatn // epsilon_0 by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
(a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by
(E2−E1).n=σε0
where ˆn is a unit vector normal to the surface at a point and σ is the surface charge density at that point. (The direction of ˆn is from side 1 to side 2.) Hence, show that just outside a conductor, the electric field is σˆn/ε0.
(b) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another. [Hint: For (a), use Gauss’s law. For, (b) use the fact that work done by electrostatic field on a closed loop is zero.]
View SolutionA hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hole is (σ2∈0)ˆn , where ˆn is the unit vector in the outward normal direction, and σ is the surface charge density near the hole,
View SolutionShow that the electric field at the surface of a charged conductor is given by →E=σ60ˆn , where σ is the surface charge density and ˆn is a unit vector normal to the surface in the outward direction.
View SolutionShow that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by (vecE_2 - vecE_1). Htan = sigma/(epsi_0) where hatn is a unit vector normal to the surface at a point and o is the surface charge density at that point. (The direction of în is from side 1 to side 2). Hence, show that just outside a conductor, the electric field is sigma/(epsi_0) hatn .
View SolutionA hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hold is (sigma)/(2pi epsilon_(0))hatn where hatn is the unit vector in the outward normal direction, and a is the surface charge density near the hole.
View SolutionShow that the electric field at the surface of a charged conductor is given by vecE = (sigma)/(epsi_(0)) hatn , where sigma is the surface charge density and hatn is a unit vector normal to the surface in the outward direction .
View SolutionShow that electric field at the surface of a charges conductor is, →E=σE0ˆn where σ is the surface charge density and ˆn is a unit vector normal to the surface in the outward direction.
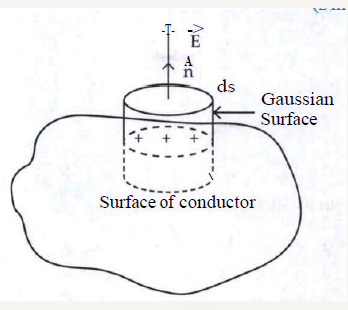
View SolutionShow that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by
(−→E2−−→E1)ˆn=σ/ε0 where ˆn isa unit vecotr normal to the surface at a point and ct is the surface charge density at that point. (The direction of ˆn is from side 1 to side 2.) Hence, show that just outside a conductor, the electric field is σˆn/ε0.
View Solution

