Question

(a ) सिद्ध करे कि किसी आवेशित सतह ( charged surface) के एक ओर से दूसरी ओर जाने के क्रम में विद्युत - क्षेत्र ${\displaystyle \overrightarrow{E}}$ के लंबवत घटक (normal component) में असांतत्य ( discontinuity ) होता है, जिसे ${\displaystyle ({\overrightarrow{E}}_2-{\overrightarrow{E}}_1)\cdot \hat{n}=\frac{\sigma }{{\in }_0}}$ द्वारा व्यक्त किया जाता है | सतह 1 से सतह 2 की ओर उस बिंदु पर अभिलम्ब एकांक सदिश ${\displaystyle =\hat{n}}$ तथा सतह के उस बिंदु पर आवेश का पृष्ठ - घनत्व = ${\displaystyle \sigma }$ है | अतः, सिद्ध करे कि आवेशित चालक के ठीक बाहर विद्युत - क्षेत्र ${\displaystyle \frac{\sigma \hat{n}}{{\in }_0}}$ है |
(b) प्रमाणित करे कि आवेशित सतह के एक ओर से दूसरी ओर जाने के क्रम में स्थिर विद्युत - क्षेत्र का स्पर्शीय घटक ( tangential component) संतत ( continuous ) रहता है |

Explanation

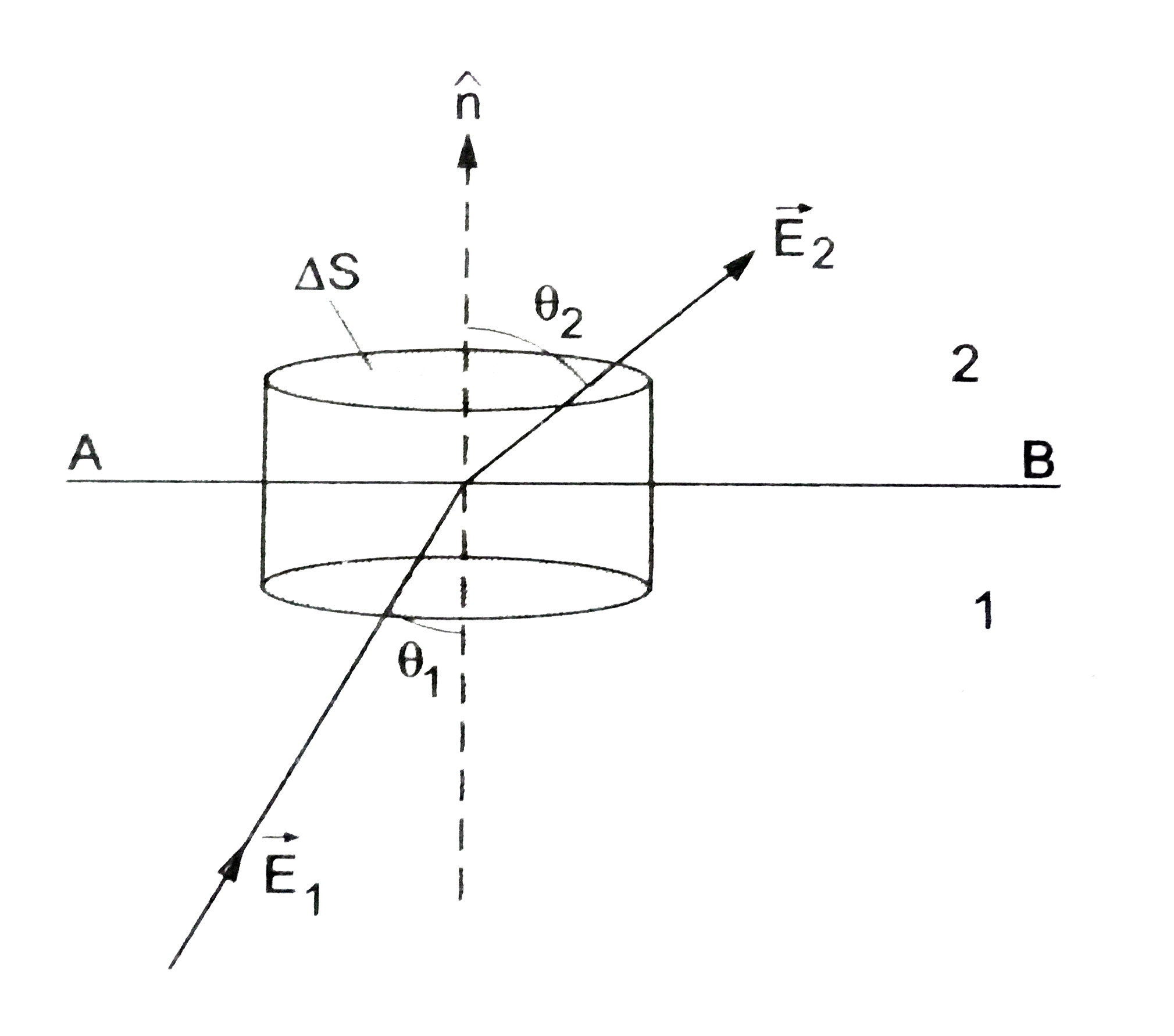
(a) परावैद्युत माध्यम 1 से 2 में जाने के क्रम में विद्युत -क्षेत्र ` vec E_ 1 ` तथा ` vec E _ 2 ` का परिमाण एवं दिशा में परिवर्तन होने का अर्थ होता है असांतत्य (discontinuity ) | चित्र में आवेशित सतह के दोनों ओर विद्युत - क्षेत्र ` vec E _ 1 ` तथा ` vec E _ 2 ` परिमाण एवं दिशाओं में दिखाएं गए है |
अब आवेशित तल AB पर खींचे गए अभिलम्ब को अक्ष मानकर एक बंद बेलनाकार तल ( closed cylindrical surface) की कल्पना करे जिसकी समतल पृष्ठ का क्षेत्रफल ` Delta S ` है | इस बंद तल से होकर गुजरनेवाला नेट विद्युत - फ्लक्स = ` phi = E _ 2 cos theta _ 2 Delta S - E _ 1 cos theta _ 1 Delta S `
` = ( vec E _ 2 * hatn - vec E _ 1 * hat n ) Delta S`
जहाँ ` hatn ` द्वारा 1 से 2 की ओर सतह पर खींचे गए अभिलम्ब की दिशा में एकांक सदिश व्यक्त है |
गॉस के प्रमेय से, ` phi = ( 1 ) /( in _ 0 ) sum q _ ( "inside") `
` therefore ( vecE _ 2 * hatn - vecE _ 1 * hatn ) Delta S = ( 1) /( in _ 0 ) ( sigma Delta S ) `
या ` ( vecE _ 2 - vec E _ 1 ) * hatn = ( sigma ) / ( in _ 0 )" " `... (1)
अब यदि आवेशित सतह AB किसी चालक की सतह ho , to चालक के भीतर विद्युत - क्षेत्र शून्य होगा, अर्थात ` E _ 1 = 0 `, अतः समीकरण (1 ) से,
` vec E _ 2 * hatn = ( sigma ) / ( in_ 0 ) `
स्पष्टतः, चालक के ठीक बहार विद्युत - क्षेत्र ,
` vecE _ 2 = ( sigma ) /( in _ 0 ) hatn ` .
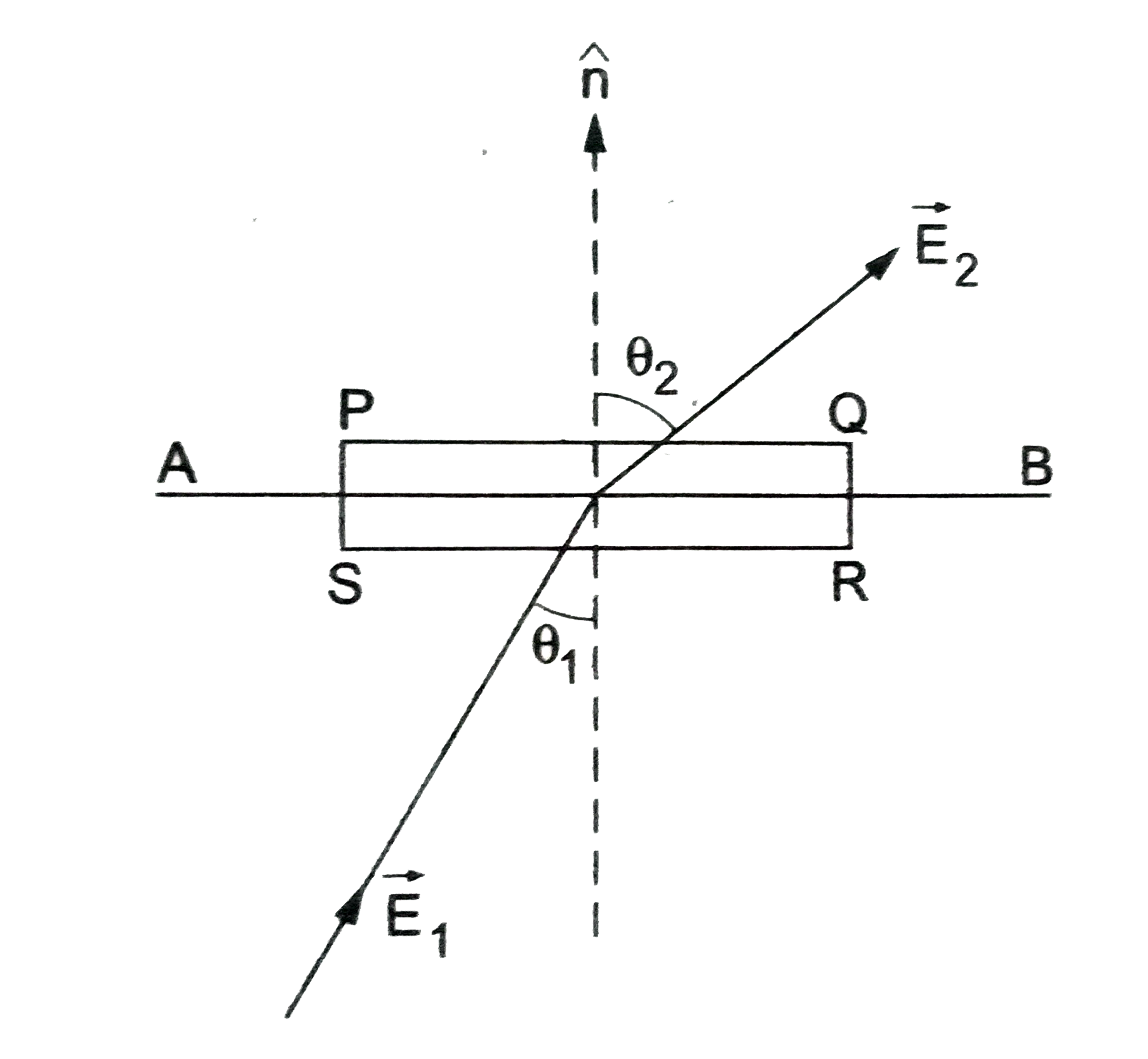
(b) परावैद्युत माध्यम के परिवर्तन से विद्युत - क्षेत्र परिमाण एवं दिशा में बदलता है | क्षेत्र के स्पर्शीय घटक का संतत होने का अर्थ है कि उनके मान में परिवर्तन नहीं होना , अर्थात चित्र के अनुसार ` E _ 1 sin theta _ 1 = E _ 2 sin theta _ 2 `.

अब एक आयताकार बंद लूप PQRS की कल्पना करे जिसमे PQ तथा RS तल AB के समांतर है | किसी आवेश को इस पथ से के एक चक्र पूरा करने में संपादित कार्य शून्य होता है, अतः
` ( W ) _ ( PQ ) + ( W) _ ( QR ) + (W) _ ( RS) + ( W) _ ( SP ) = 0 `
या ` E _ 2 sin theta _ 2 * P Q + W - E _ 1 sin theta _ 1 * RS - W = 0 " " [ because W _ ( QR ) = - W _ ( SP ) ] `
या ` E _ 1 sin theta _ 1 = E _ 2 sin theta _ 2 `
स्पष्टतः क्षेत्र रेखा के अपवर्तन में क्षेत्र का स्पर्शीय घटक अपरिवर्तित रहता है |