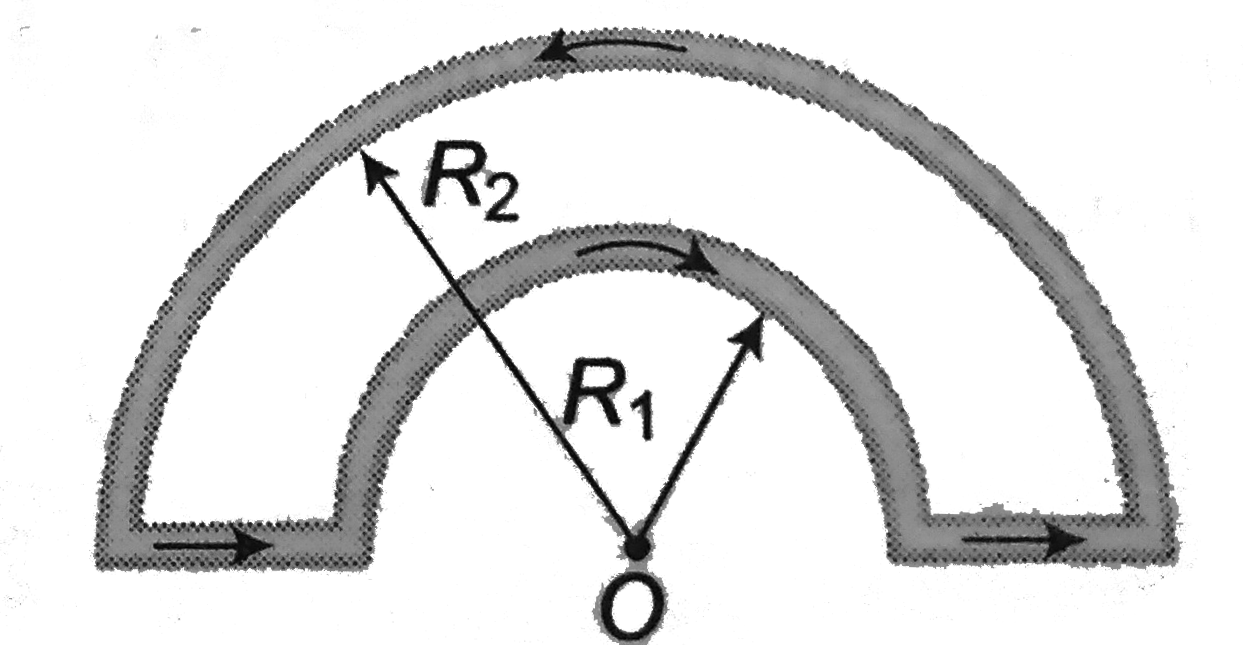
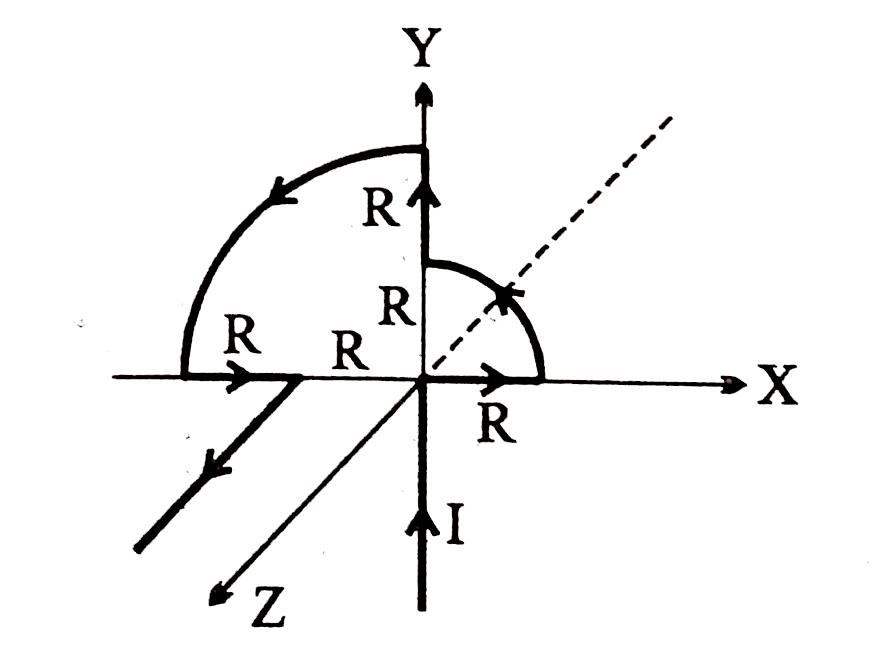
In the loop shown, the magnetic induction at the point 'o' is

A
μ0I8(R1−R2R1R2)
B
μ0I8(R1+R2R1R2)
C
μ0I8(R1R2R1+R2)
D
0
Video Solution
Text Solution
The correct Answer is:B
By using formula B=μ04πIr(θ0)
|
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM Book:PHYSICS WALLAHChapter:MOVING CHARGES AND MAGNETISM Exercise:NEET PAST 5 YEARS QUESTIONS
Explore 12 Videos
- MOVING CHARGES AND MAGNETISM Book:PHYSICS WALLAHChapter:MOVING CHARGES AND MAGNETISM Exercise:NEET PAST 5 YEARS QUESTIONS
Explore 12 Videos
- MOTION IN A STRAIGHT LINEBook:PHYSICS WALLAHChapter:MOTION IN A STRAIGHT LINEExercise:NEET Past 5 Years Questions
Explore 5 Videos
- OSCILLATIONS Book:PHYSICS WALLAHChapter:OSCILLATIONS Exercise:NEET PAST 5 YEARS QUESTIONS
Explore 5 Videos
Similar Questions
Knowledge Check
In the given figure the magnetic induction at the point O is
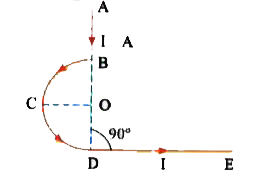 Aμ0I4πaBμ0I4r+μ0I2πrCμ0I4r+μ0I4πrDμ0I4r−μ0I4πr
Aμ0I4πaBμ0I4r+μ0I2πrCμ0I4r+μ0I4πrDμ0I4r−μ0I4πrIn the figure shown, the magnetic field at the point O is
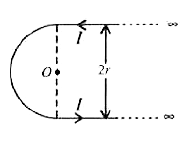 Aμ04Ir(π+l)Bμ04Ir(π+2)Cμ04Ir(π−2)Dμ04Ir
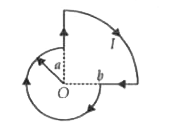
Aμ04Ir(π+l)Bμ04Ir(π+2)Cμ04Ir(π−2)Dμ04IrThe magnetic induction at centre O Fig.
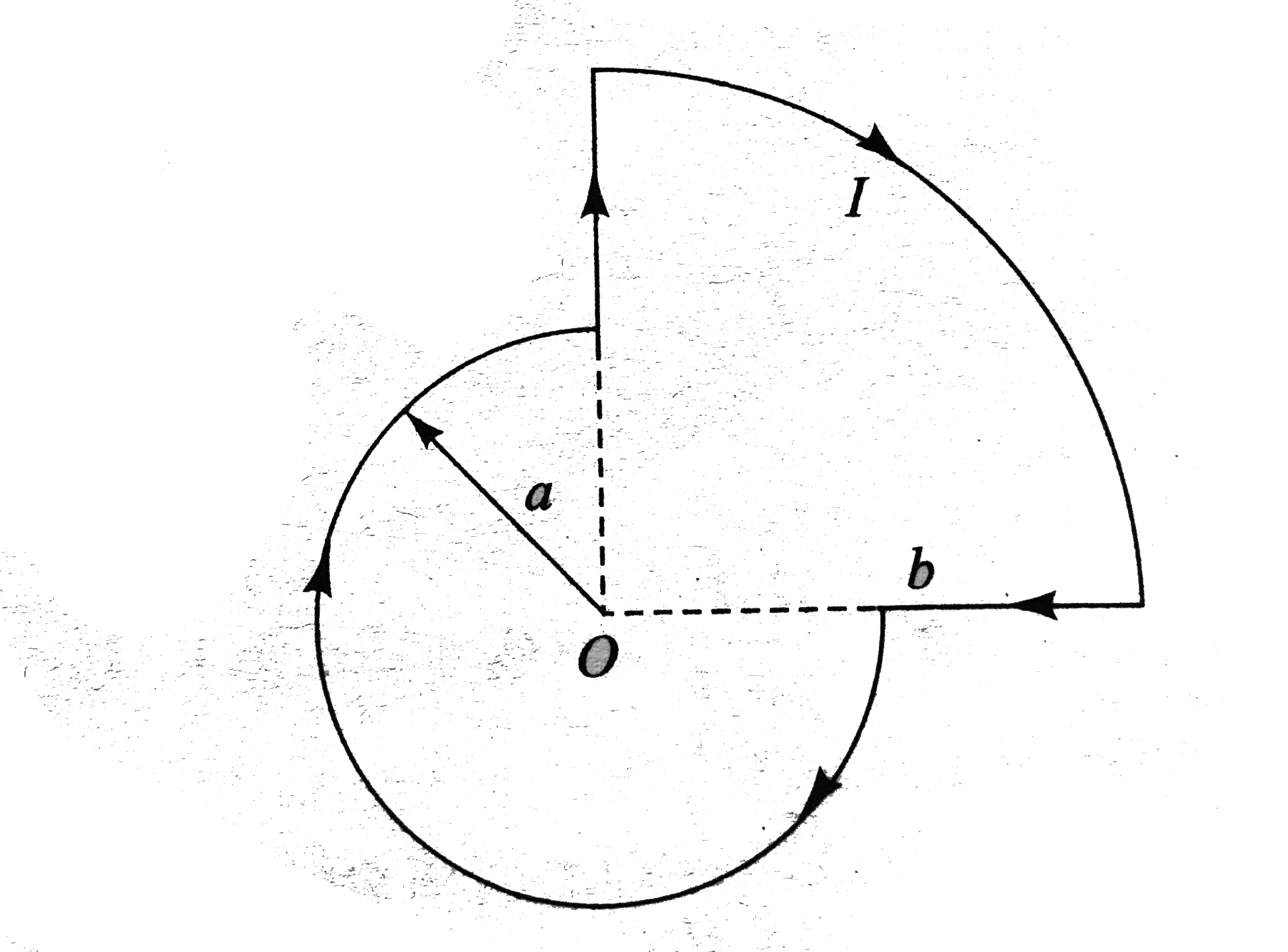 Aμ0I2a+μ0I2b⊗B3μ0I8a+μ0I8b⊗C3μ0I8a−μ0I8b⊗D3μ0I8a+μ0I8b⊙
Aμ0I2a+μ0I2b⊗B3μ0I8a+μ0I8b⊗C3μ0I8a−μ0I8b⊗D3μ0I8a+μ0I8b⊙
Find the magnetic induction at the origin in the figure shown.
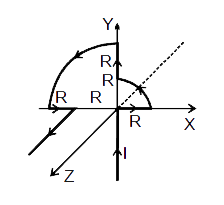
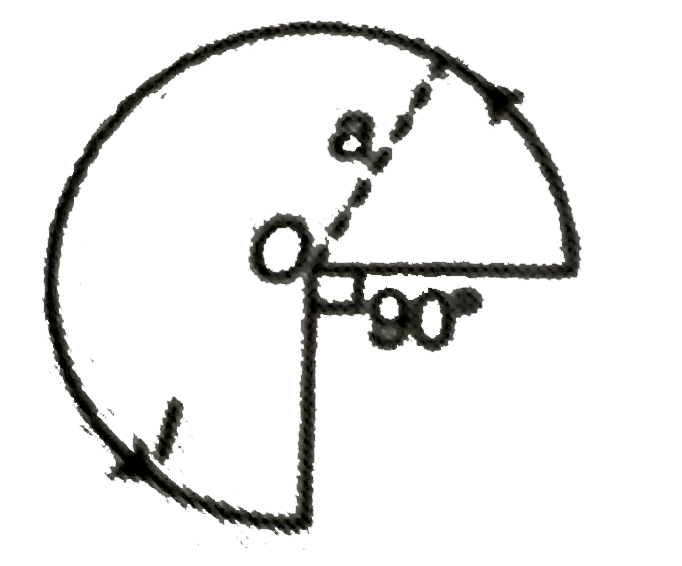
View SolutionThe magnetic induction at the centre O in the figure shown in
View SolutionFor the arrangment as shown in the figure, the magnetic induction at the centre is
View SolutionThe magnetic induction at center O as shown in the figure is
View SolutionAn infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R meter. The magnetic induction at the centre of loop is
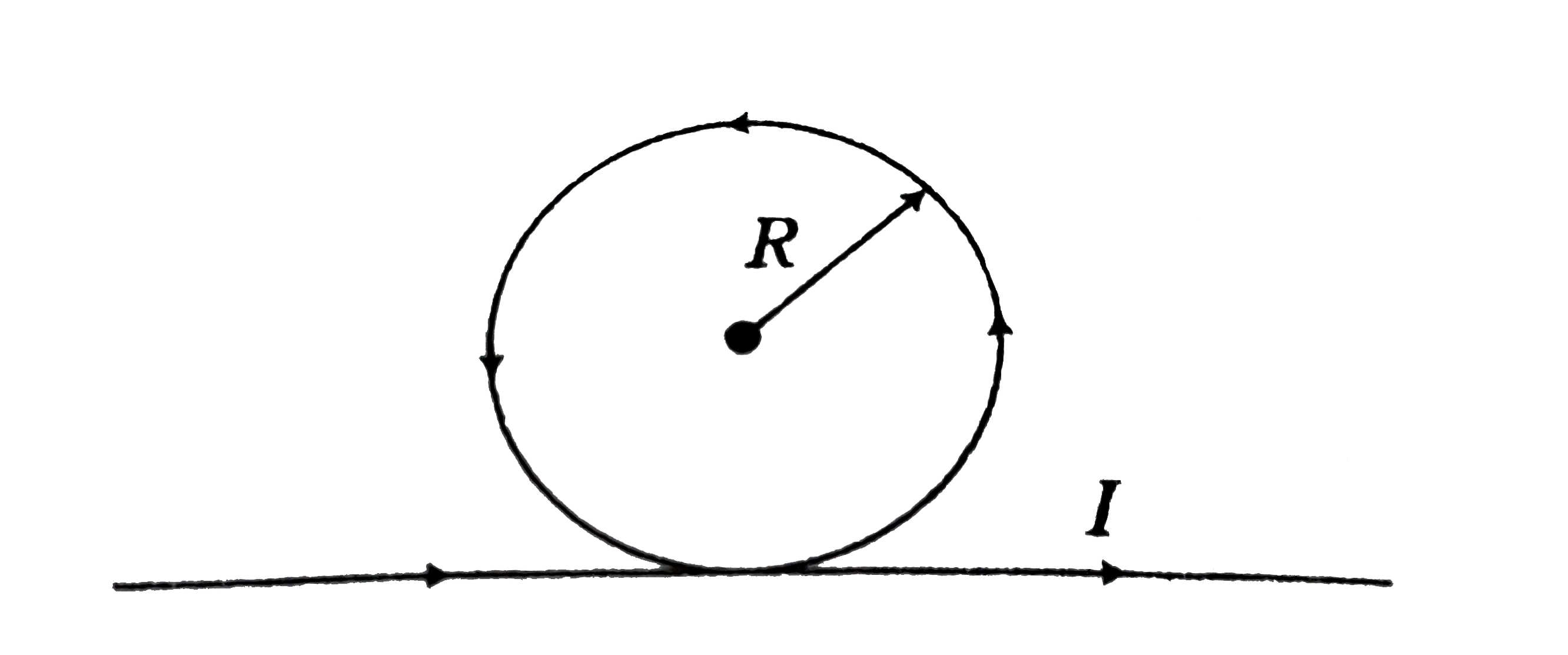
View Solution
 .
.