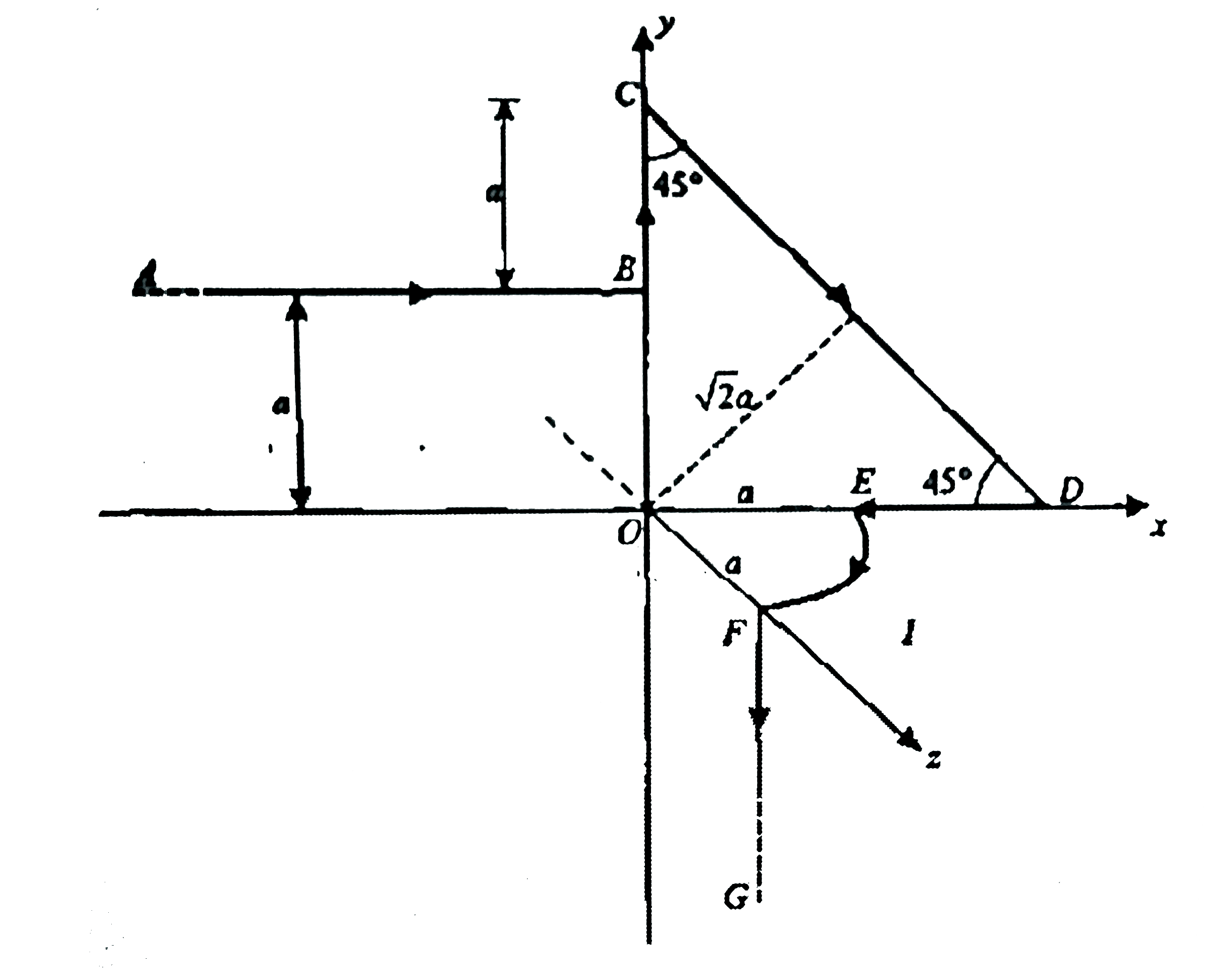
Find the magnetic induction the origin in the shown
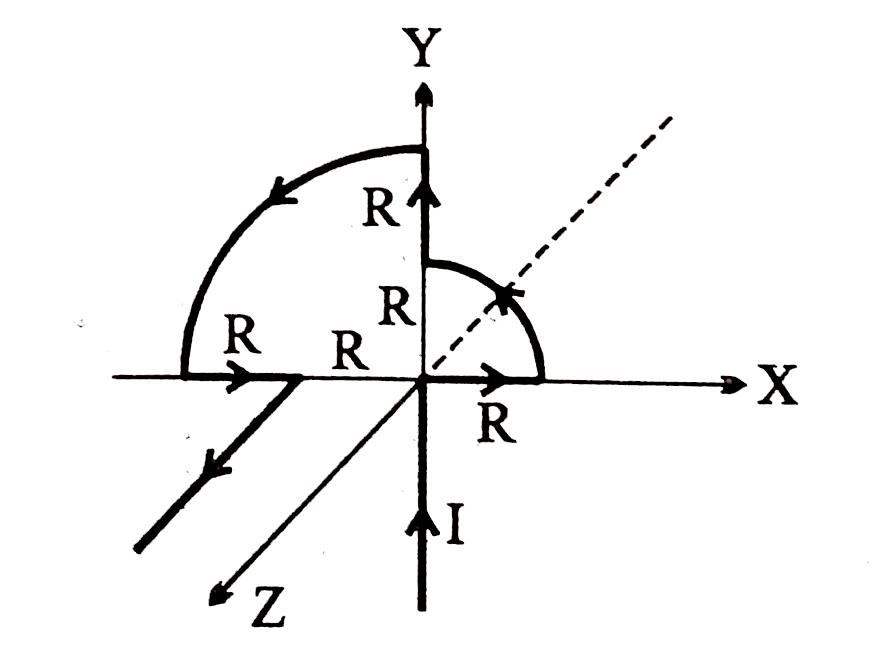 .
.
Video Solution
Text Solution
The correct Answer is:μ0I4R(34ˆk+1πˆj)
B1=0,B2=0,B3=μ04πIR×π2ˆk
B4=0,B5=μ04πIRˆj
→B=→B1+→B2+→B3+→B4+→B5+→B6+→B7
→B=μ04R[12+12]ˆk+μ04πIRˆj=μ0I4R[34ˆk+1πˆj]
 .
.
|
Similar Questions
Knowledge Check
Find the magnetic induction at the origin in the figure shown.
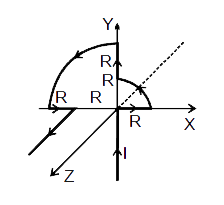 Aμ0I2R(34ˆk+1πˆj)Bμ0I4R(34ˆk+1πˆj)Cμ0I3R(34ˆk+1πˆj)Dμ0I4R(12ˆk+1πˆj)
Aμ0I2R(34ˆk+1πˆj)Bμ0I4R(34ˆk+1πˆj)Cμ0I3R(34ˆk+1πˆj)Dμ0I4R(12ˆk+1πˆj)Magnetic induction is a
AScalar quantityBVector quantityCBoth (a) and (b)DNone of the aboveFind the magnetic field at the origin in the fig. Shown in fig.
 Aμ0I4R(34ˆk+1πˆj)Bμ0I4R(32ˆk+1πˆj)Cμ0I4R(34ˆk+12πˆj)DNone of these
Aμ0I4R(34ˆk+1πˆj)Bμ0I4R(32ˆk+1πˆj)Cμ0I4R(34ˆk+12πˆj)DNone of these
Find the magnetic induction at point O, if the current carrying wire is in the shape shown in the figure
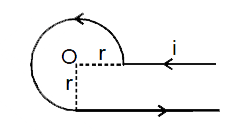
View SolutionWhat is magnetic induction ?
View SolutionFind the magnetic induction at point P due to a current carrying wire AB as shown in figure-4.31
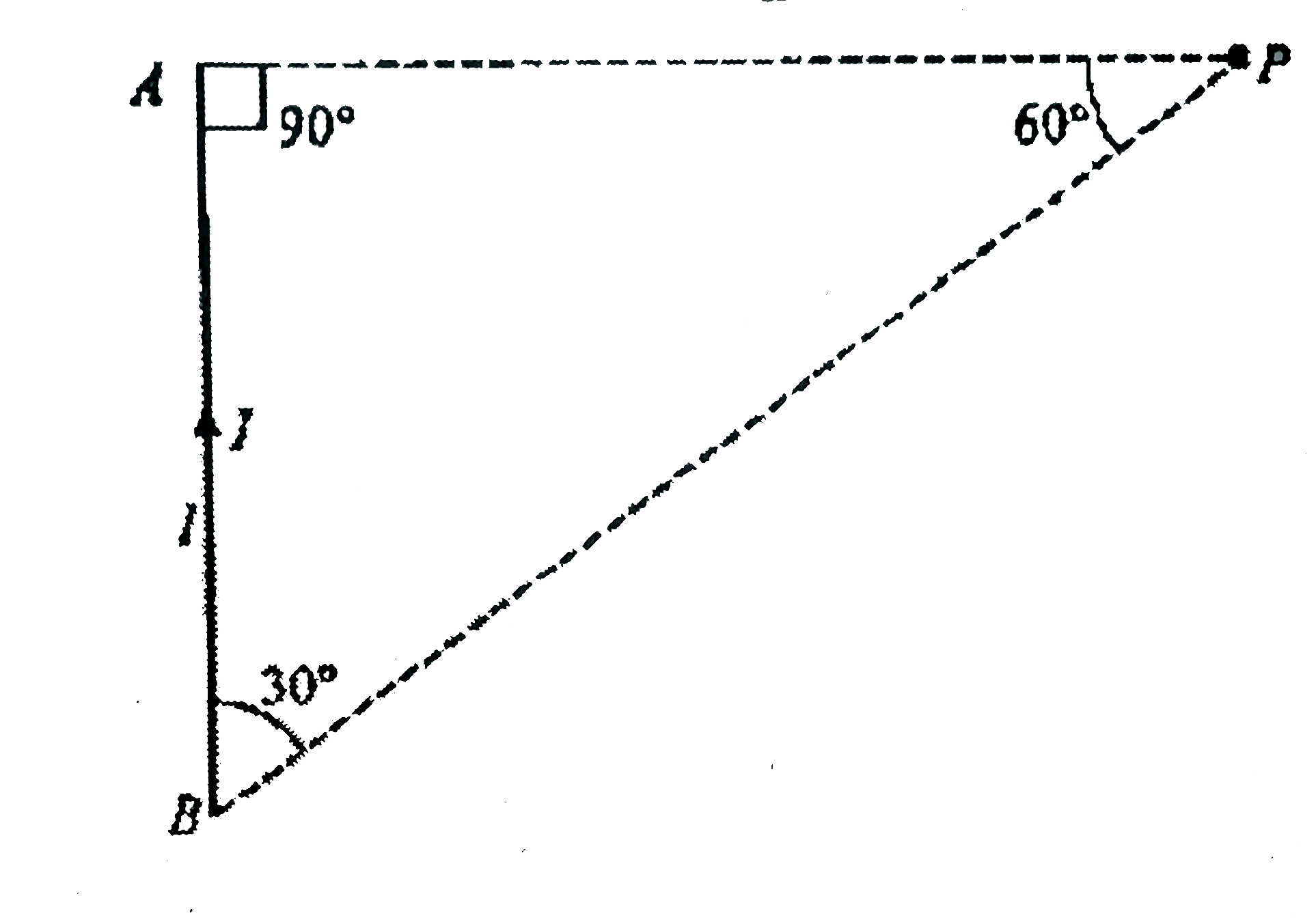
View SolutionFind magnetic induction at P due to wire:
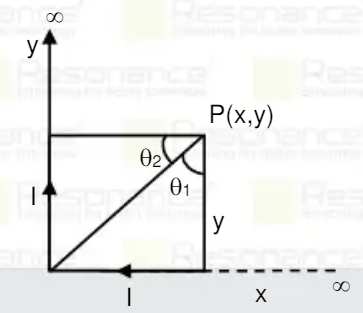
View SolutionFind the magnetic induction at point O, if the current carrying wire is in the shape shown in the figure.
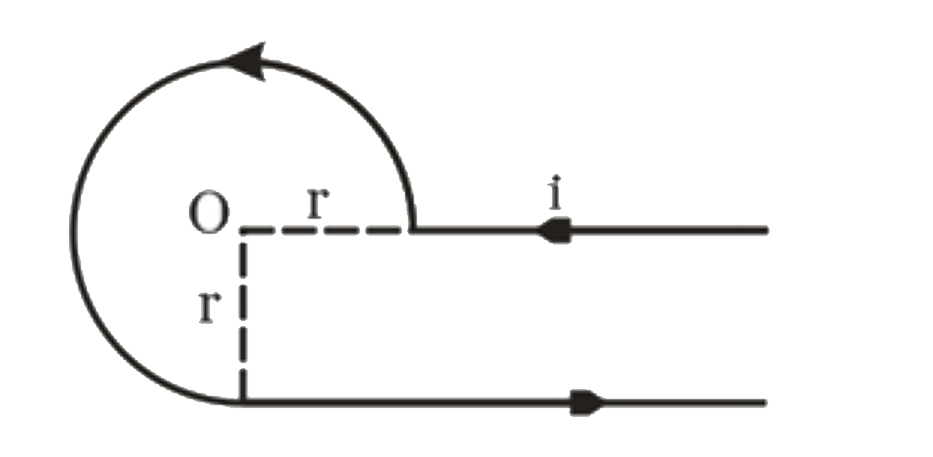
View Solution
 .
.