Test if the following equation is dimensionally correct: h=(sScosθrpg) where h= height, S= surface tension, p= density, r=radius, and g= acceleration due to gravity.
s=12at2
v=√T/m
t=2hg
a=v2r
The correct Answer is:C
a.S=12at2,[L]=[LT−2][T2]=[L]
b.V=√Tm
[LT−1]=[MLT−2ML−1]1/2=[LT−1]
c=t=2hg,[t]=[T]
[2hg]=[LLT−2]=T2 not equal to [T]
d.A=V2r
⇒[LT−2]=[LT−1]2[L]=[LT−2]
Topper's Solved these Questions
- UNITS AND MEASUREMENTS Book:PHYSICS WALLAHChapter:UNITS AND MEASUREMENTS Exercise:NEET PAST 5 YEARS QUESTIONS
Explore 10 Videos
- UNITS AND MEASUREMENTS Book:PHYSICS WALLAHChapter:UNITS AND MEASUREMENTS Exercise:NEET PAST 5 YEARS QUESTIONS
Explore 10 Videos
- THERMODYNAMICSBook:PHYSICS WALLAHChapter:THERMODYNAMICSExercise:NEET Past 5 Years Questions
Explore 14 Videos
- WAVE OPTICSBook:PHYSICS WALLAHChapter:WAVE OPTICSExercise:Neet Past 5 Years Questions
Explore 16 Videos
Similar Questions
Which of the following equations is dimensionally incorrect ?
Where t=time, h = height, s = surface tension, θ = angle, p= density, a, r = radius, g = acceleration due to gravity, v = volume, p = pressure, W = work done, T = torque, ε=permittivity, E = electric field, J = current density, L = length.
View SolutionCheck the correctness of the relation h=2σcosθr2dg, where h is height , sigam is surface tension, θ is angle of contact, r is radius, d is density and g in acceleration due to gravity.
View Solution
Knowledge Check
Given as : h=2Scosθrρg where S is the surface tension of liquid, r is the radius of capillary tube. ρ is the density and g is acceleration due to gravity then dimensional formula for S is:
A[ML0T−2]B[M0LT−2]C[ML2T−2]D[M0L0T−3]The Bernoulli's equation is given by P+12ρv2+hρg=k. Where P= pressure, ρ= density, v= speed, h=height of the liquid column, g= acceleration due to gravity and k is constant. The dimensional formula for k is same as that for:
AVelocity gradientBPressure gradientCModulus of elasticityDThrustThe binding energy of an object of mass m placed on the surface of the earth r is (R = radius of earth, g = acceleration due to gravity)
AmgR/2Bmg RCmgR4DmgR8
A particle is taken to a height R above the earth's surface, where R is the radius of the earth. The acceleration due to gravity there is
View SolutionThe pressure at a depth h in a liquid of density d is given by pressure = __ , where g is the acceleration due to gravity.
View Solution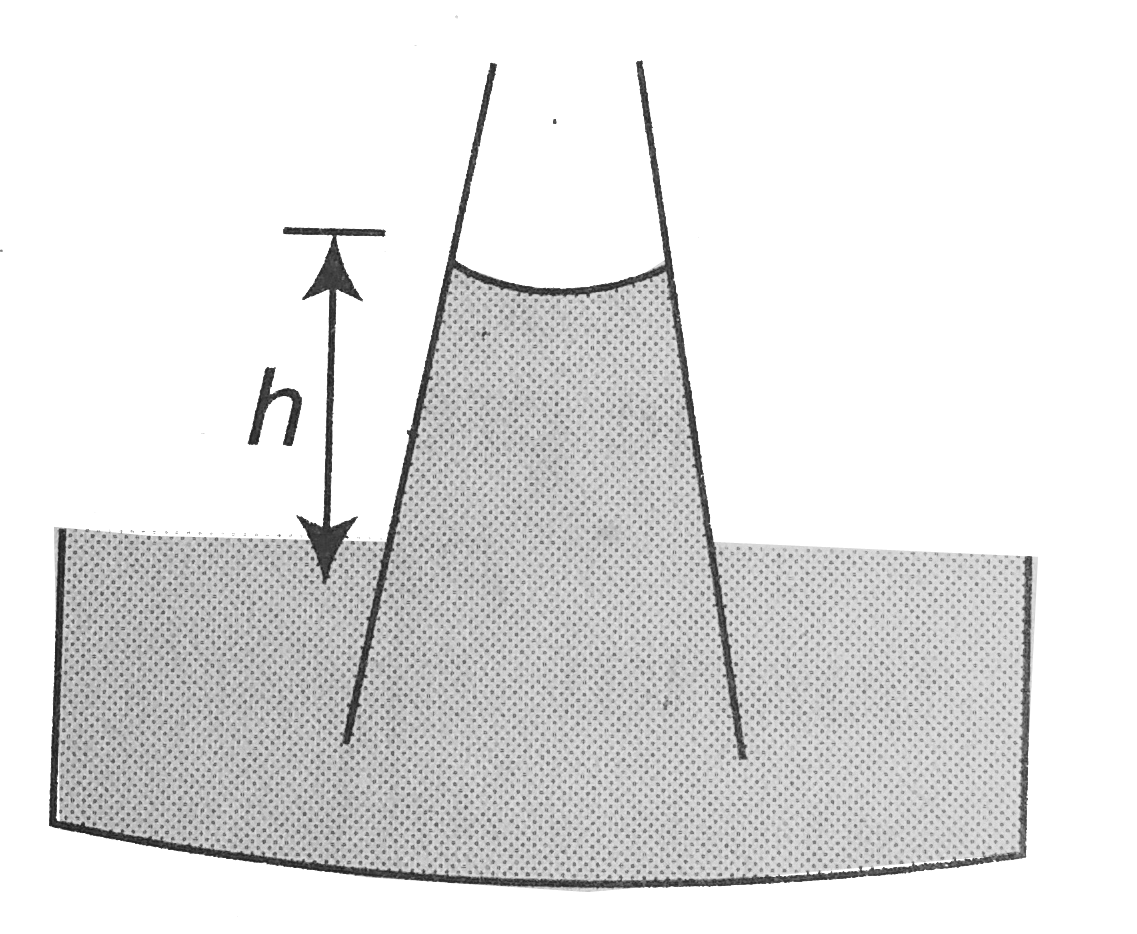
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:
View SolutionAccording to Bernoulli's theorem pd+v22+gh = constant is (P is pressure, d is density, h is height, v is velocity and g is acceleration due to gravity)
View SolutionThe absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
View Solution

