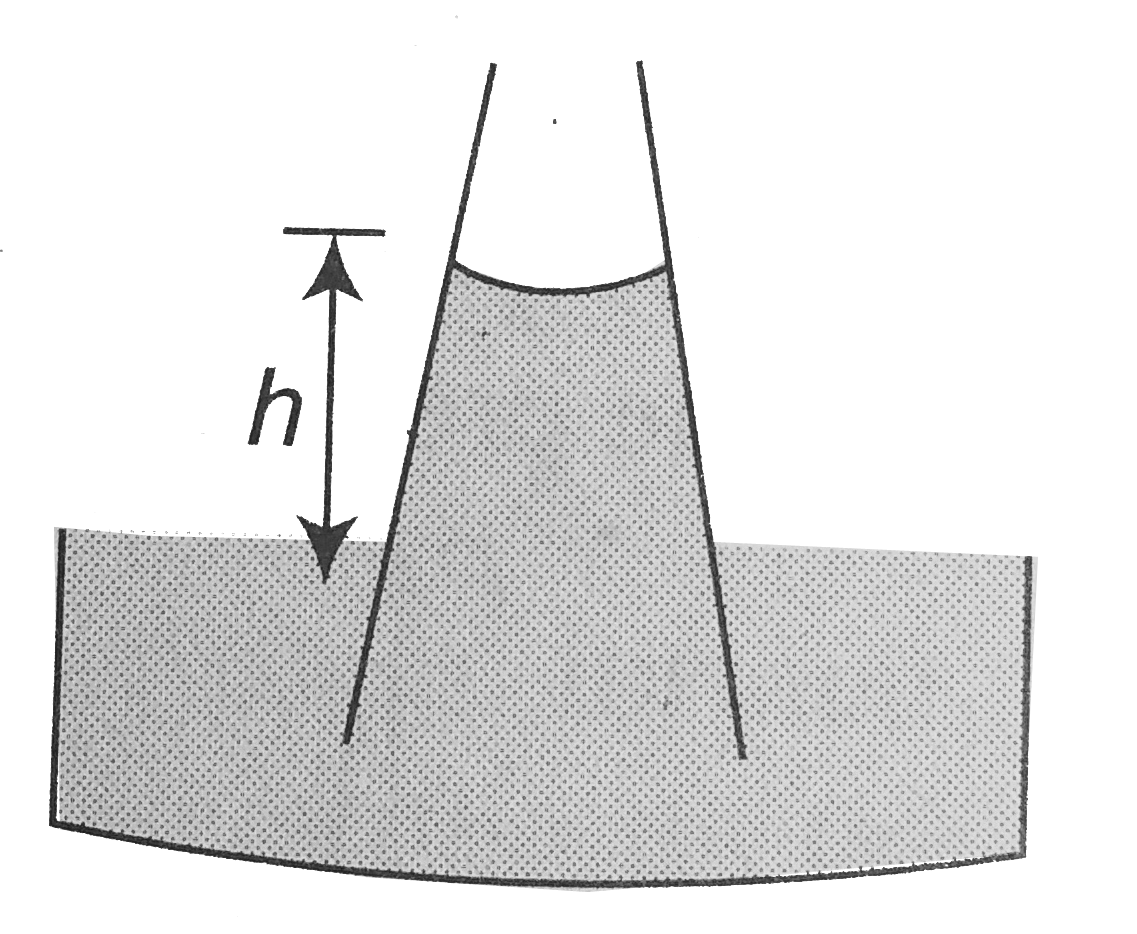
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:
greater than 2Trρg
equal to 2Trρg
less than 2Trρg
of any value depending upon act.
The correct Answer is:B

2πrT=πr2 ρgh⇒h=2Trρg
But weight of liquid in tapered tube is more than uniform tube of radius r, then the order to balance h<h1
h<2Trρg
Topper's Solved these Questions
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Viscosity
Explore 29 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Problems Based On Mixed Concepts
Explore 34 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Surface Tension And Surface Energy
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Chapter Test
Explore 29 Videos
Similar Questions
When a capillary tube of radius r is dipped vertically in a liquid of surface tension T, the liquid rises to a height h in the tube above the level outside the tube . If the angle of contact is θ the density of the liquid is ρ then the pressure difference between the points A and B is

View SolutionIf a capillary tube is dipped into liquid and the levels of the liquid inside and outside are same, then the angle of contact is
View Solution
Knowledge Check
The graph between the mass of liquid inside the capillary and radius of capillary is
A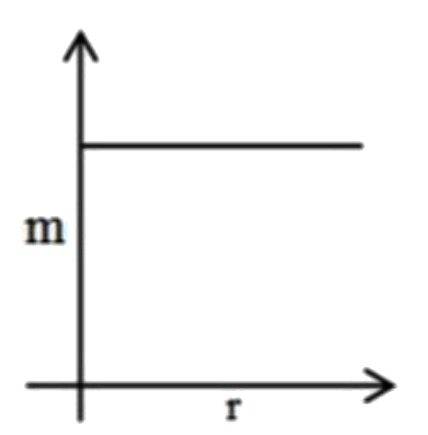 B
B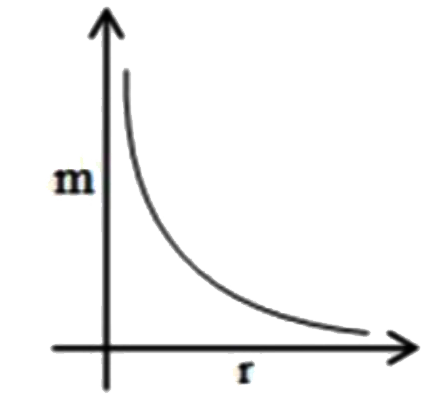 C
C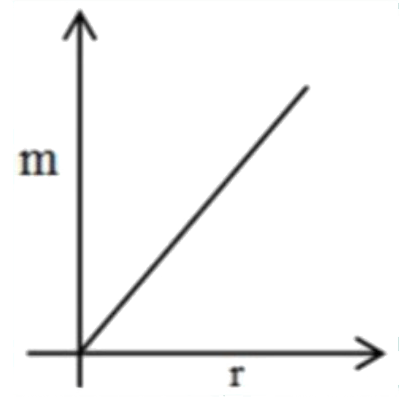 D
D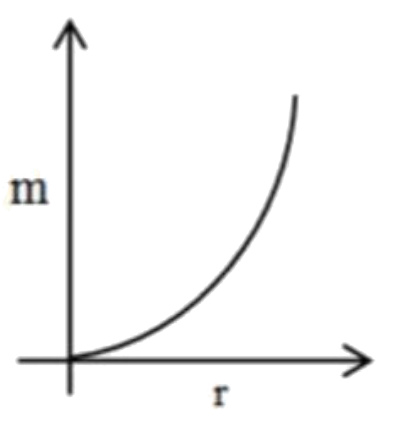
Given as : h=2Scosθrρg where S is the surface tension of liquid, r is the radius of capillary tube. ρ is the density and g is acceleration due to gravity then dimensional formula for S is:
A[ML0T−2]B[M0LT−2]C[ML2T−2]D[M0L0T−3]The liquid in the capillary tube will rise if the angle of contact is
A120∘B90∘CobtuseDacute
The radius of the bore of a capillary tube is r and the angle of contact of the liquid is θ . When the tube is dipped in the liquid , the radius of curvature of the meniscus of liquid rising in the tube is
View SolutionThe angle of contact of a liquid in a capillary tube is 60∘. The shape of the meniscus is
View SolutionIf a capillary tube is dipped into liquid and the levels of the liquid inside and outside are same, then the angle of contact is
View SolutionThe height of liquid column in capillary tube is h the radius of capillary tube is r.ρ is the density of liquid , g is acceleration due to gravity and θ is angle of contact . The surface tension of the liquid is ,
View SolutionThe radii of the two column is U-tube are r1 and r2(>r1). When a liquid of density ρ (angle of contact is 0∘)) is filled in it, the level different of liquid in two arms is h. The surface tension of liquid is
(g= acceleration due to gravity)
View Solution

