The absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
ρgh
Pa+ρgh
Pa−ρgh
Pa2ρgh
The correct Answer is:B
Step by step video, text & image solution for The absolute pressure at a depth h below the surface of a liquid of density rho is [Given P_(a) = atmospheric pressure, g = acceleration due to gravity] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTEChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - B
Explore 23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTEChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - C
Explore 15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTEChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:TRY YOURSELF
Explore 41 Videos
- MAGNETISM AND MATTER Book:AAKASH INSTITUTEChapter:MAGNETISM AND MATTER Exercise:ASSIGNMENT (SECTION D)
Explore 26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTEChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment(Section-D)
Explore 12 Videos
Similar Questions
Knowledge Check
The pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depthThe pressure in a liquid at a given depth below the surface :
Ais always exerted downward.Bis the same in all directions .Cequals the total weight of liquid above the depth.Ddepends upon the amount of liquid below the depth .If the atompspheric pressure is Pa then the jpressure P at depth a below the surface of a liquid of density ρ open to the atmosphere is
APa−ρgh2BPa−ρghCPa+ρghDP1+ρgh2
Find the total pressure inside a sperical air bubble of radius 0.2 mm. The bubble is at a depth 5 cm below the surface of a liquid of density 2×103 kg m−3 and surface tension 0.082 N m−1. (Given : atmospheric pressure = 1.01 ×105Nm−2)
Hint : Pi=Po+2SR
Po = atmospheric pressure + gauge pressure of liquid column.
View SolutionAn air bubble is formed at depth h below the surface of water. The pressure inside the bubble is-
(P0= atmospheric pressure, r = radius of bubble)
View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
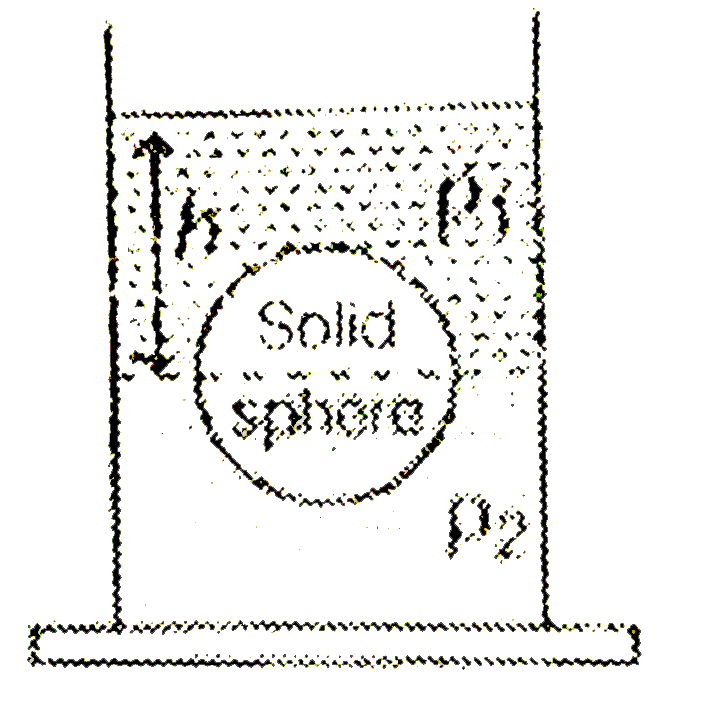
View SolutionCalculate the pressure inside a small air bubble of radus r situated at a depth h below the free surface of liquids of densities ρ1 and ρ2 and surface tennsions T1 and T2. The thickness of the first and second liquids are h1 and h2 respectively. Take atmosphere pressure =P0.

View SolutionAn air bubble of radius r in water is at a depth h below the water surface at some instant. If P is atmospheric pressure, d and T are density and surface tension of water respectivley . the pressure inside the bubble will be :
View Solution

