If the vectors →a,→b and →c from the sides BC,CA and AB respectively of aΔABC then Solution in Tamil
→a,→b+→b.→c+→c.→a=0
→a×→b=→b×→c=→c×→a
→a.→b=→b.→c=→c.→a
→a×→b+→b×→c+→c×→a=→0
The correct Answer is:B
By triangle law →a+→b+→c=→0
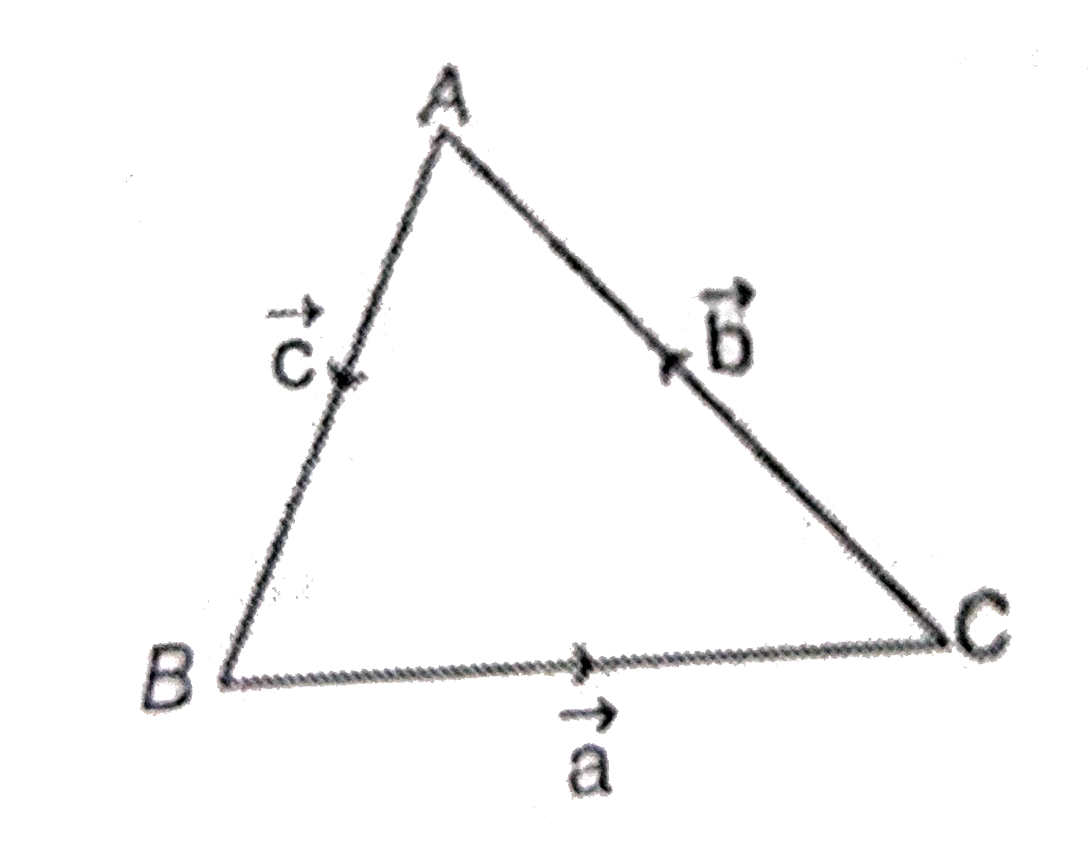
Taking cross product by →a,→b,→c respectively
→a×(→a+→b+→c)=→a×→0=→0
⇒→a×→a+→a×→b+→a×→c=→a
⇒→a×→b=→c×→a
Similarly →a×→b=→b×→a
∴→a×→b=→b×→a
Similar Questions
If →a,→b,→c are non-coplanar unit vectors such that
→a×(→b×→c)=(→b+→c)√2, then the angle between →a and →b is
View SolutionIf →A=(1,1,1),→C=(0,1,−1) are given vectors then a vectors →B satisfying the equations →A×→B=→C and →A. →B=3 is ………
View SolutionIf vectors →a,→b,→C are coplanar then show that
∣∣ ∣ ∣∣→a→b→c→a.→a→a.→b→a.→c→b.→a→b.→b→b.→c∣∣ ∣ ∣∣
View SolutionIf −a,−b,−c are three vectors such that ∣∣−a∣∣=1,∣∣∣−b∣∣∣=2,∣∣−c∣∣=3,and−a.−b.=−b.−c=−c.−a=0, then ∣∣∣[−a−b−c]∣∣∣=
View SolutionFor any three vectors →a,→band→c, prove that vectors →a−→b,→b−→c,→c−→a are coplanar.
View SolutionA,B,C and d are four points in a plane with position vectors →a,→b,→c and →d respectively such that (→a−→d).(→b−→c)=(→b−→d)(→c−→a)=0 The point D then is the .... of the ΔABC
View SolutionLet →A,→B,→C be vectors of length 3, 4, 5, respectively Let →A be perpendicular to →B+→C,→B to →C+→A and →C to →A+→B then the length of vector →A+→B+→C is .......
View Solutionif →a,→b and →c are unit vectors satisfying
∣∣→a−→b∣∣2+∣∣→b−→c∣∣2+|→c−→a|2=9
∣∣2→a+5→b+5→c∣∣ is equal to
View Solution