If the vectors →a,→b and →c from the sides BC,CA and AB respectively of aΔABC then
→a,→b+→b.→c+→c.→a=0
→a×→b=→b×→c=→c×→a
→a.→b=→b.→c=→c.→a
→a×→b+→b×→c+→c×→a=→0
The correct Answer is:B
By triangle law →a+→b+→c=→0
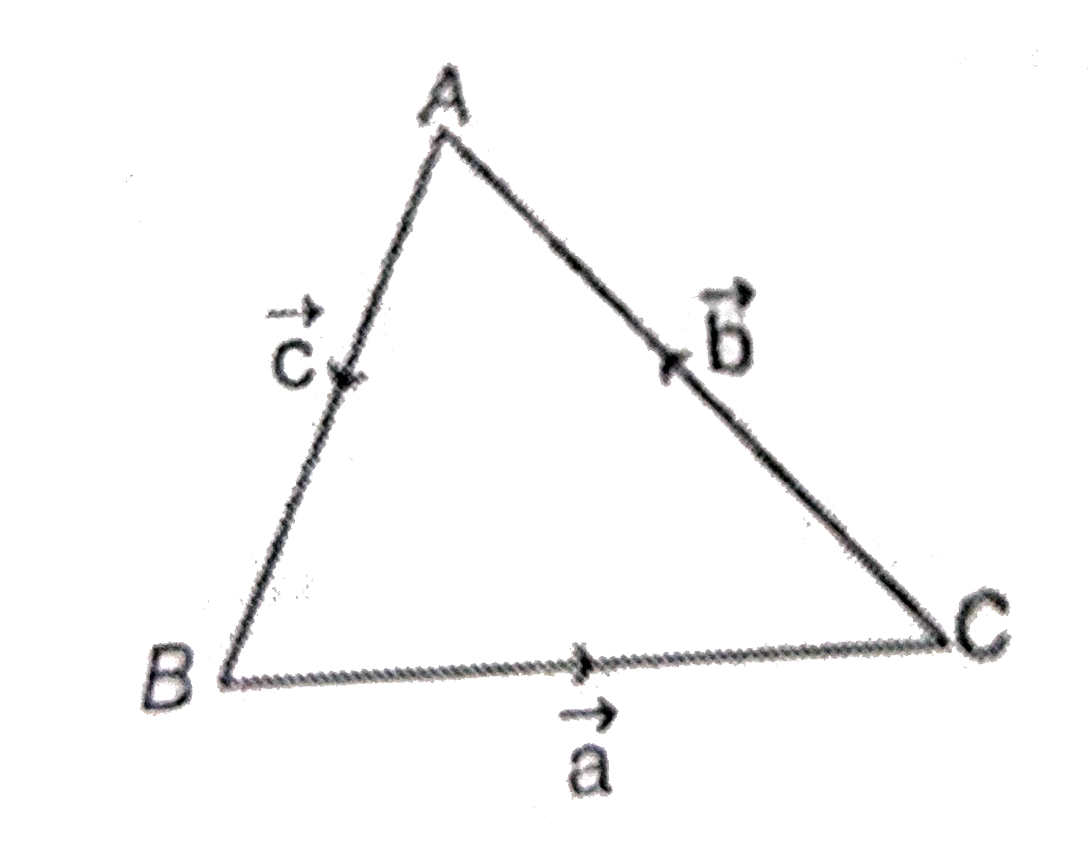
Taking cross product by →a,→b,→c respectively
→a×(→a+→b+→c)=→a×→0=→0
⇒→a×→a+→a×→b+→a×→c=→a
⇒→a×→b=→c×→a
Similarly →a×→b=→b×→a
∴→a×→b=→b×→a
Topper's Solved these Questions
- VECTOR ALGEBRABook:IIT JEE PREVIOUS YEARChapter:VECTOR ALGEBRAExercise:Vector Product of Two Vectors (Objective Questions I) (Assertion and Reason)
Explore 1 Video
- VECTOR ALGEBRABook:IIT JEE PREVIOUS YEARChapter:VECTOR ALGEBRAExercise:Vector Product of Two Vectors (Objective Questions I) (Passage Based Problems)
Explore 2 Videos
- VECTOR ALGEBRABook:IIT JEE PREVIOUS YEARChapter:VECTOR ALGEBRAExercise:Vector Product of Two Vectors (Objective Questions I)
Explore 12 Videos
- TRIGONOMETRICAL RATIOS AND IDENTITIESBook:IIT JEE PREVIOUS YEARChapter:TRIGONOMETRICAL RATIOS AND IDENTITIESExercise:HEIGHT AND DISTANCE
Explore 10 Videos
Similar Questions
Knowledge Check
If the vectors ¯a,¯b and ¯c from the sides BC, CA and AB, respectively, of ΔABC, then
A¯a.¯b+¯b.¯c+¯c.¯a=0B¯aׯb=¯bׯc=¯cׯaC¯a.¯b=¯b.¯c=¯c.¯aD(¯aׯb)+(¯bׯc)+(¯cׯa)=¯0Let →a,→b,→c form sides BC,CA and AB respectively of a triangle ABC then
Aa.b+b.c+c.a=0Ba×b=b×c=c×aCa.b=b.c=c.aDa×b+b×c+c×a=0Let the vectors →a,→b,→c and →d be such that
(→a×→b)×(→c×→d)=→0. If P1 and P2 are planes determined by the pairs of vectors →a,→b and oerset(→)(c),→d respectively then the angle between P1 and P2 isA0Bπ/4Cπ/3Dπ/2
If →u,→v,→w are three non- coplanar unit vectors and α,β,γ the angles between →u and →v,→v and →w,→w and →u respectively and →x,→y,→z are unit vectors along the bisectors of the angles α,β,γ respectively . Prove that
[→x×→y→y×→z→z×→x]=116[→u→v→w]2 sec2.α2 sec2.β2 sec2.γ2
View SolutionIf the vectors →b,→c,→d are not coplanar then prove than the vectors (→a×→b)×(→c×→d)+(→a×→c)×(→d×→b)
+(→a×→d)×(→b×→c) is parallel to →a
View SolutionA,B,C and d are four points in a plane with position vectors →a,→b,→c and →d respectively such that (→a−→d).(→b−→c)=(→b−→d)(→c−→a)=0 The point D then is the .... of the ΔABC
View SolutionLet →a,→b and →c be three non-zero vectors such that no two of them are collinear and (→a×→b)×→c=13∣∣→b∣∣|→c|→a.
If 0 is the angle between vectors →b and →c then a value of sin 0 is
View SolutionIf →a,→b and →c are unit coplanar vectors then the scalar triple product [2→a−→b2→b−→c2→c−→a] is
View Solution
