A,B,C and d are four points in a plane with position vectors $\to a, \to b, \to c$ and $\to d$ respectively such that $(\to a - \to d) . (\to b - \to c) = (\to b - \to d) (\to c - \to a) = 0$ The point D then is the .... of the $Δ A B C$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:Orthocentre

As $(\to a - \to d) . (\to b - \to c) = (\to b - \to d) . (\to c - \to a) = 0$
$\Rightarrow A D ⊥ B C and B D ⊥ C A$
which clearly represents from figure that D is orthocentre of $Δ A B C$

|

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

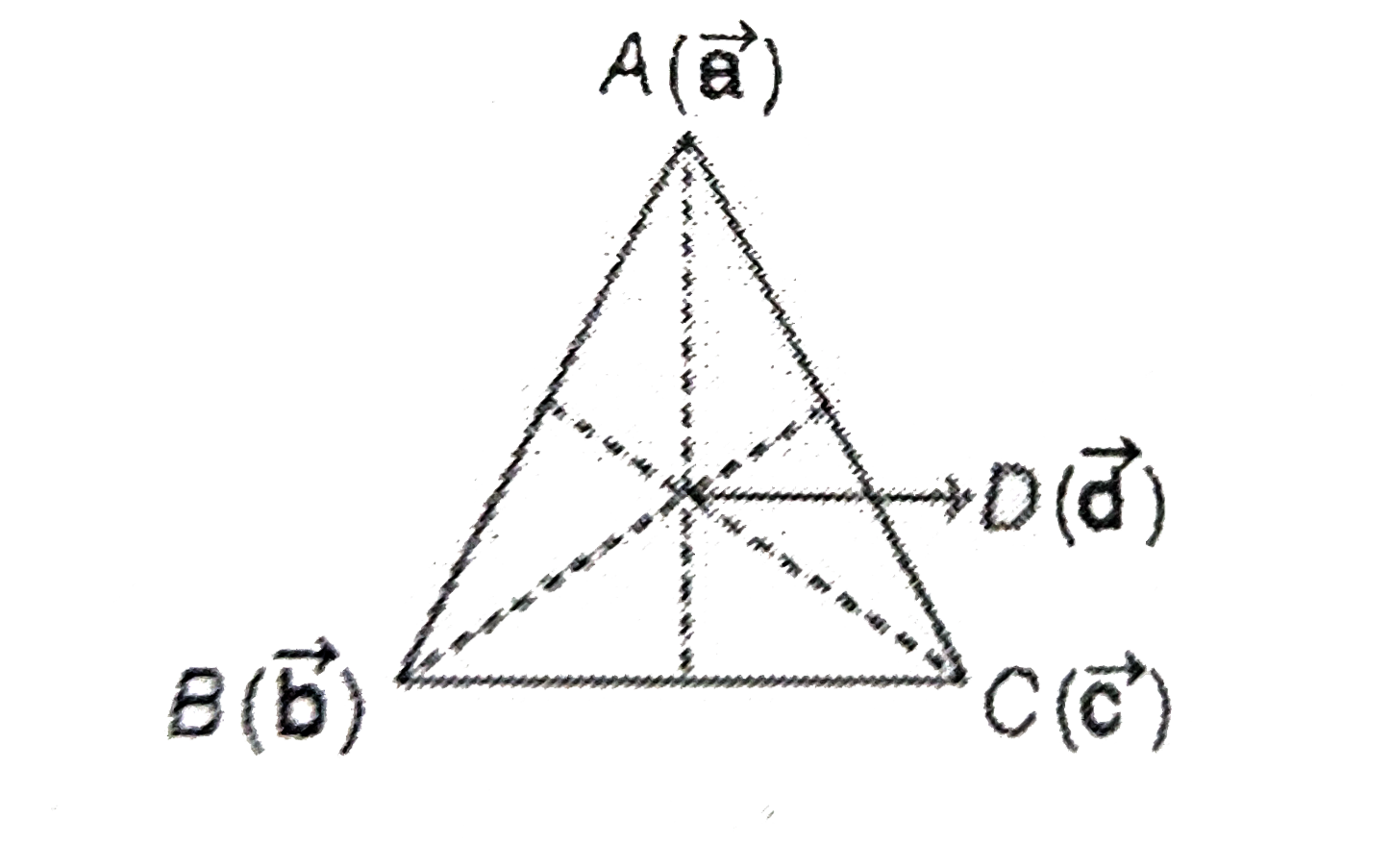
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $\to a, \to b, \to c and \to d$ are the unit vectors such that
$(\to a \times \to b) . (\to c \times \to d) = 1 and \to a, \to c = . \frac{1}{2},$ then
A $\to a, \to b, \to c$ are non -coplanar
B $\to a, \to b, \to d$ are non- coplanar
C $\to b, \to d$ are non-parallel
D $\to a, \to d$ are parallel and $\to b, \to c$ are parallel
Question 2 - Select One
if $\to a, \to b and \to c$ are unit vectors then
${∣ ∣ \to a - \to b ∣ ∣}^{2} + {∣ ∣ \to b - \to c ∣ ∣}^{2} + {| \to c - \to a |}^{2}$ does not exceed
A4
B9
C8
D6
Question 3 - Select One
If $\to a, \to b and \to c$ are three non- coplanar vectors then
$(\to a + \to b + \to c) . [(\to a + \to b) \times (\to a + \to c)]$ equals
A0
B $[\to c \to b \to c]$
C $[\to c \to b \to c]$
D $[\to a \to b \to c]$

IIT JEE PREVIOUS YEAR-VECTOR ALGEBRA-Scalar Product of two vectors (Fill in the Blanks)

Home
Ask Doubt
Profile