Consider the quadratic equation ax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
The least value of a is
Option 1: 4
Option 2: 6
Option 3: 7
Option 4: 5Solution in Tamil
4
6
7
5
The correct Answer is:4
az2−bx+c=0
Let f(x)=ax2−bx+cbe
the correspoding quadratic expression and α,β be the roots of f(x)=0.
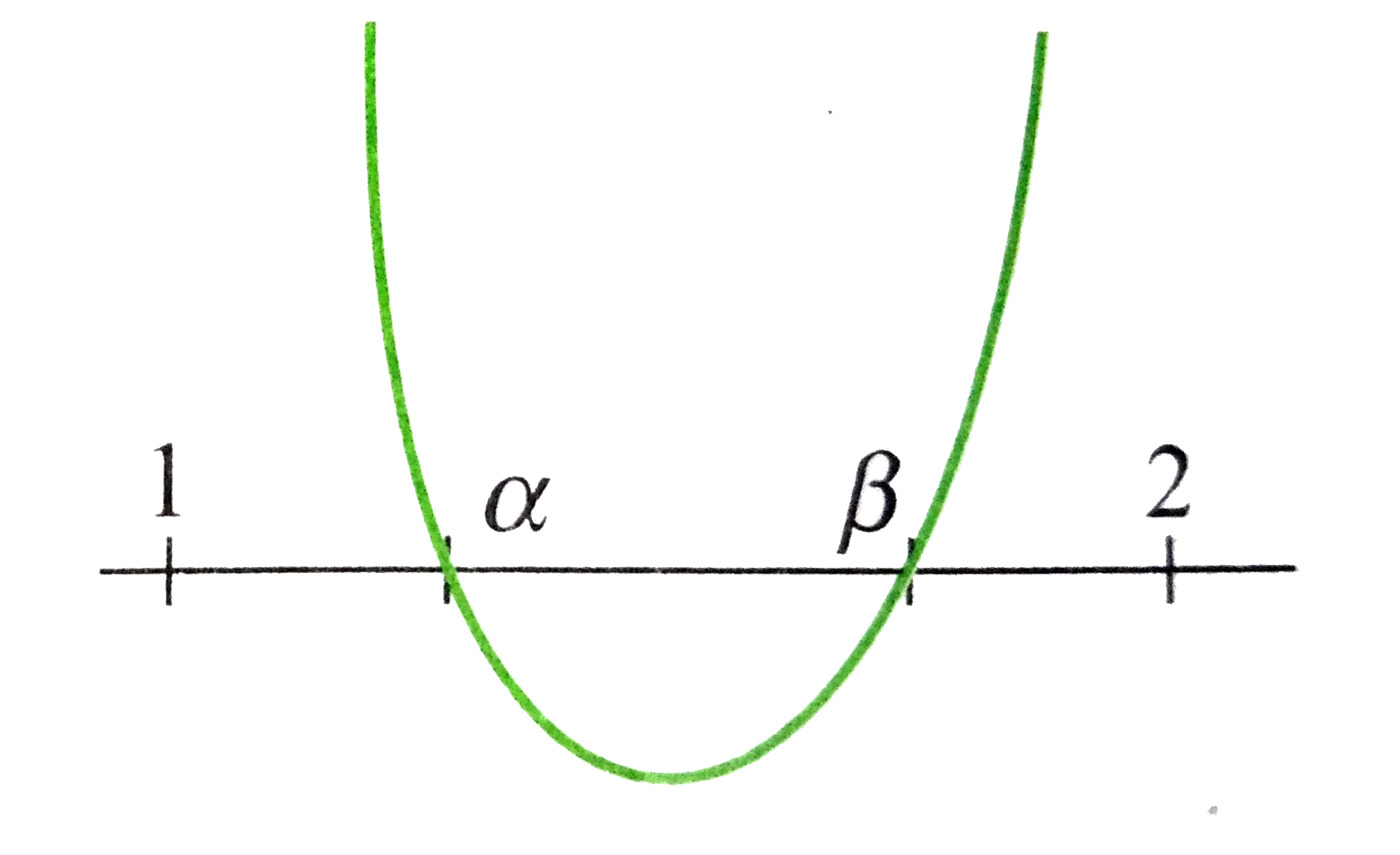
Then, f(x)=a(x−α)(x−β)
Now, af(1)>0,af(2)>0,1<b2a<2,b2−4ac>0
⇒a(1−α)(1−β)>0,a(2−α)(2−β)>0,2a<b<4a,b2−4ax>0
⇒a2(1−α)(1−β)(2−α)(2−β)>0
⇒a2(1−α)(1−β)(2−α)(2−β)>0
As f(x) and f(2) both are integers and f(1)>0, and f(2)>0, so
f(1)f(2)>0
⇒f(1)f(2)>1
⇒1≥a2(α−1)(2−α)(β−1)(2−β) (1)
Now, (α−1)+(2−α)2>((α−1)(2−α))1/2
⇒(α−1)(2−α)≤14
Similarly,
(β−1)(2−β)≤14
⇒(α−1)(2−α)(β−1)(2−β)<116
As α≠β, so α2>1 (Using (1))
⇒a>5
⇒b2>20candb>10⇒b≥11
Also, b2>100⇒c>5⇒c≥6
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Matrix)
6 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Numerical)
43 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Multiple)
38 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year
4 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
12 Videos
Similar Questions
Match the following for the equation x2+a|x|+1=0 where, a is a parameter.

View SolutionIf x=2+223+213, then the value of x3−6x2+6x is:
View Solutionif c≠0 and the equation p2x=ax+c+bx−c has two equal roots, then p can be
View Solutionabout to only mathematics
View SolutionThe equation of the plane which has the property that the point Q(5,4,5) is the reflection of point P(1,2,3) through that plane, is ax+by+cz=d where a,b,c,d∈N. Find the least value of (a+b+c+d).
View SolutionIf ax2−bx+c=0 have two distinct roots lying in the interval (0,1);a,b,∈N, then the least value of a , is
View SolutionConsider the quadrationax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
The least value of a is
View SolutionConsider the quadrationax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
The least value of b is
View SolutionConsider the quadrationax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
The least value of c is
View SolutionA quadratic equation ax2+bx+c=0has two distinct real roots, if….
View SolutionConsider the quadrationax2−bx+c=0,a,b,c∈N which has two distinct real roots belonging to the interval (1,2).
The least value of b is
View Solutionयदि द्विघात समीकरण ax2+bx+6=0 के दो भिन्न वस्तविक मूल नहीं है, तब 2a+b का न्यूनतम मान है-
View SolutionIf ax2−bx+c=0 have two distinct roots lying in the interval (0,1);a,b,∈N, then the least value of a , is
View SolutionIfax2−bx+c=0 has two distinct roots lying in the interval (0,1),a,b,c∈N. Then
View SolutionThe quadratic equation ax2+bx+c=0 has real roots if:
View Solution
