If (x+2) is a common factor of (px2+qx+r) and (qx2+px+r) then a) p=q or p+q+r=0 b)p=r or p+q+r=0 c) q=r or p+q+r=0 d)p=q=−12rSolution in Tamil
|d|≤|D|
|d|≥|D|
|d|=|D|
None of these
The correct Answer is:1
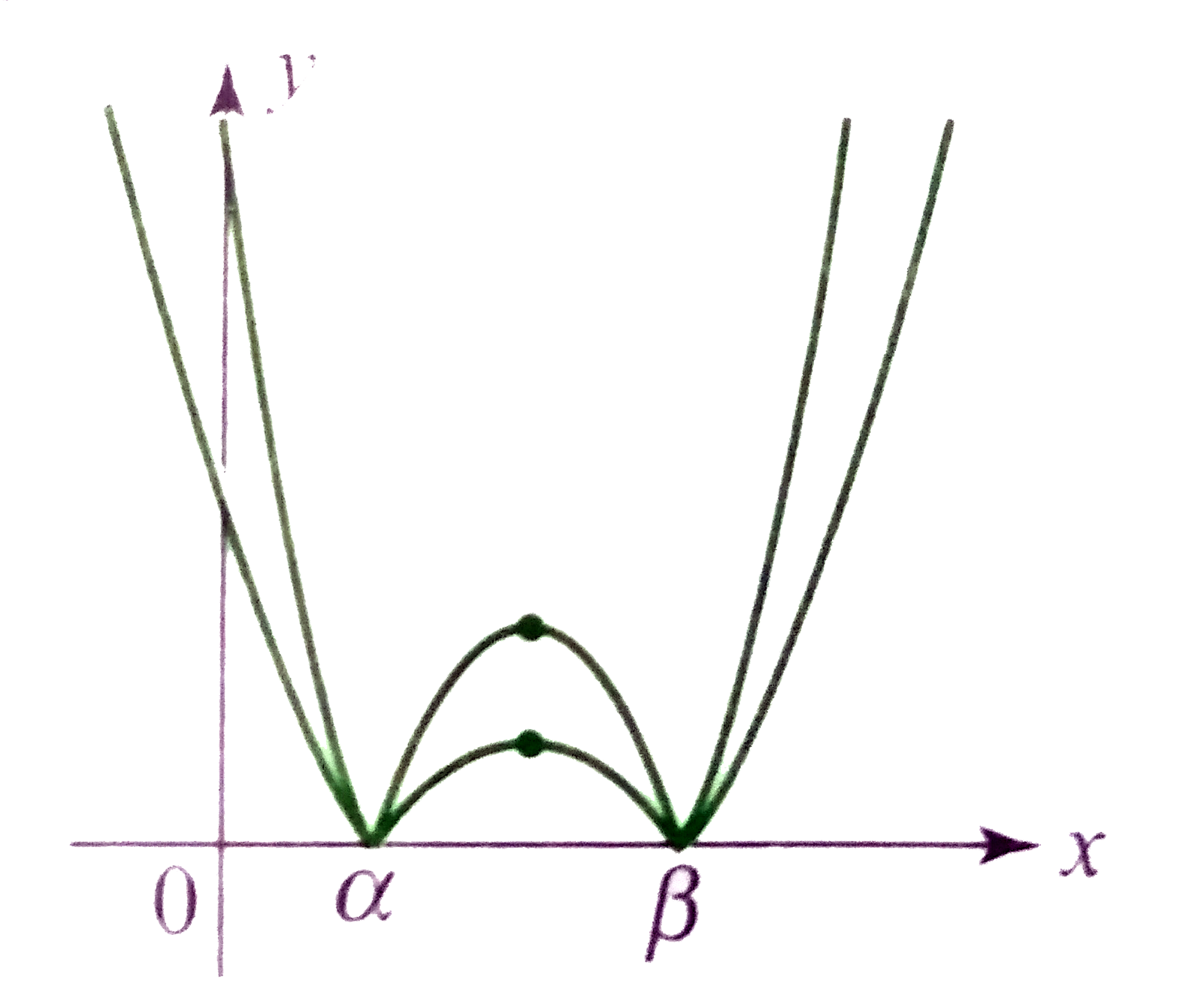
∣∣px2+qx+r∣∣≤∣∣Px2+Qx+R∣∣∀x∈R (1)
Form the graph we can see that this is possible only when both equations have same roots.
Thus, α and β are roots of Px2+Qx+R=0 and also of
px2+qx+r=0
So, from (1),
|p||x−α||x−β|≤|P||x−α||x−β|
⇒|p|≤|p|
Also ∣∣∣4pr−q24p∣∣∣≤∣∣∣4PR−Q24p∣∣∣
⇒|d|≤∣∣∣pP∣∣∣|D|
⇒|d|≤|D| (∵|p|≤|P|)
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Matrix)
6 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Numerical)
43 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Multiple)
38 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year
4 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
12 Videos
Similar Questions
Match the following for the equation x2+a|x|+1=0 where, a is a parameter.

View SolutionIf x=2+223+213, then the value of x3−6x2+6x is:
View Solutionif c≠0 and the equation p2x=ax+c+bx−c has two equal roots, then p can be
View Solutionabout to only mathematics
View SolutionThe equation of the plane which has the property that the point Q(5,4,5) is the reflection of point P(1,2,3) through that plane, is ax+by+cz=d where a,b,c,d∈N. Find the least value of (a+b+c+d).
View SolutionIf (x+2) is a common factor of (px^(2)+qx+r) and (qx^(2)+px+r) then a p=q or p+q+r=0 b p=r or p+q+r=0 c) q=r or p+q+r=0 d p=q=-(1)/(2)r
View SolutionProve that pxq−r+qxr−p+rxp−q>p+q+r,wherep,q,r are distinct andx≠1.
View SolutionIf p,q,r>0 and p!=q!=r such that,f(x)=px^(2)+2qx+r,g(x)=qx^(2)+2rx+p,f(x)=0 and g(x)=0 has a common root.
View SolutionIf the equations px^(2)+qx+r=0 and rx^(2)+qx+p=0 have a negative common root then the value of (p-q+r)=
View SolutionThe roots of the equation (q−r)x2+(r−p)x+p−q=0 are (A) r−pq−r,1 (B) p−qq−r,1 (C) q−rp−q,1 (D) r−pp−q,1
View SolutionIf p,q,rεR and the quadratic equation px2+qx+r=0 has no real roots, then (A) p(p+q+r)>0 (B) (p+q+r)>0 (C) q(p+q+r)>0 (D) p+q+r>0
View SolutionShow that the equations px2+qx+r=0 and qx2+px+r=0 will have a common root if p+q+r=0 or, p=q=r.
View Solution|(0,p-q,p-r),(q-p,0,q-r),(r-p,r-q,0)|=
View SolutionIf px3+qx2+rx+s=0 is a R.E .of second type then
p=s,q=r
p=-s,q=-r
p=s,q=-r
p=-s ,q=r
View SolutionIf (x+2) is a common factor of (px2+qx+r) and (qx2+px+r) then (a) p=q or p+q+r=0 (b)p=r or p+q+r=0 (c) q=r or p+q+r=0 (d)p=q=−12r
View Solutionरेखीय (p−q)x+(q−r)y+(r−p)=0
(q−r)x+(r−p)y+(p−q)=0
व (r−p)x+(p−q)y+(q−r)=0 है
View Solution
