Consider the equaiton 2+∣∣x2+4x+3∣∣=m,m∈R Set of all values of m so that the given equation have two solutions is Option 1: (3,∞) Option 2: (2,∞) Option 3: {2}∪(3,∞) Option 4: None of theseSolution in Tamil

A

(3,∞)

B

(2,∞)

C

{2}∪(3,∞)

D

None of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:3

Given equations is 2+∣∣x2+4x+3∣∣=m
∴∣∣x2+4x+3∣∣=m−2
Given equation is meaningful if m≥2 (1)
∴x2+4x+3=±(m−2)
∴x2+4x+5−m=0orx2+4x+1+m=0
∴x=−4±√16−4(5−m)2orx=−4±√16−4(1+m)2
∴x=−2±√m−1orx=−2±√3−m
For four distinct solutions m−1≥0 and 3−m≥0
∴m∈(2,3) [Using (1)]
For two solutions m−1≥0and3−m≤0⇒m≤0⇒m≥3
or m−1≤0and3−m≤0, not possible
or m=2 [Using (1)]
∴m∈{2}∪(3,∞)
Form three solutions, exactly one equation must given equal roots.
∴m=1and3−m≥0⇒ no values of m (as m≥2)
or m=3andm≥1⇒m=3
Alternate method:
Let us draw the graph of f(x)=∣∣x2+4x+3∣∣
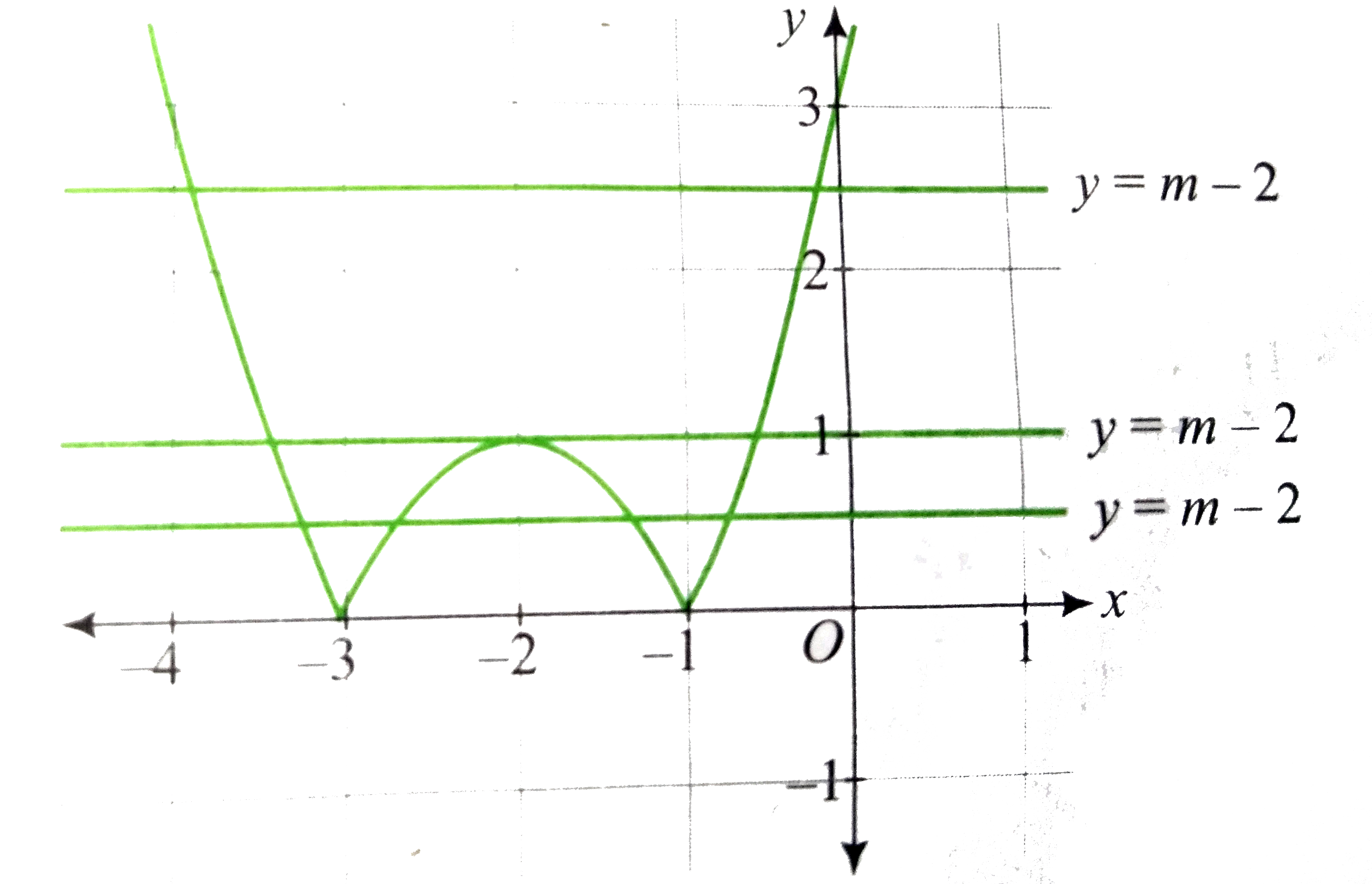
ocr_image
Now equations is |(x+1)(x+3)|=m−2
From the graph.
(1) for three solution m−2=1⇒m=3
(2) for four solutions
0<m−2<1⇒2<m<3
(3) for only tow solutions
m−2=0orn−>1
⇒m=2orm>3

|
Updated on:21/07/2023
Class 12MATHSQUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions