Question

If $x^4+2k{x}^3+x^2+2kx+1=0$
has exactly tow distinct positive and two distinct negative roots, then find the possible real values of k.

Explanation

The given equation is `(x^(2) + (1) /(x^(2) )) + 2k (x + (1)/(x)) + 1 = 0`
or `(x + (1) /(x))^(2) + 2k (x + (1)/(x)) + 1 = 0`
Putting `x + (1)/(x) = t`, the above equation to `t^(2) + 2kt - 1 = 0`
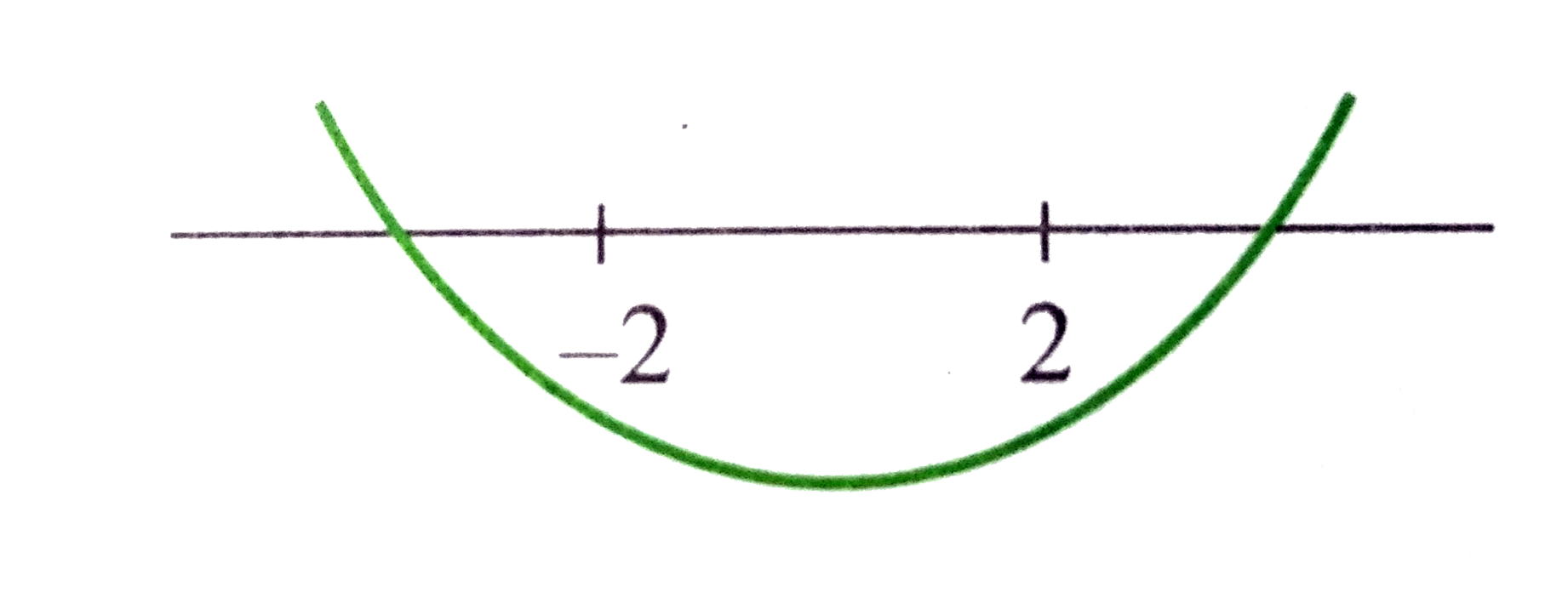
Now, we know that `x +(1)/(x) ge 2 if x gt 0, and x + (1)/(x) lt - 2 if x lt 0` .
So, one of the rots of `t^(2) + 2kt - 1 = 0` will lie in `(-infty, -2)` and other root in `(2, infty)`.
`therefore f(-2) lt 0`
`rArr 4 - 4k - 1 lt 0`
or `k gt 3//4`
And `f(2) lt 0`
`rArr 4 + 4k - 1 lt0`
or `k lt - 3//4`
Henc, k `in phi.`