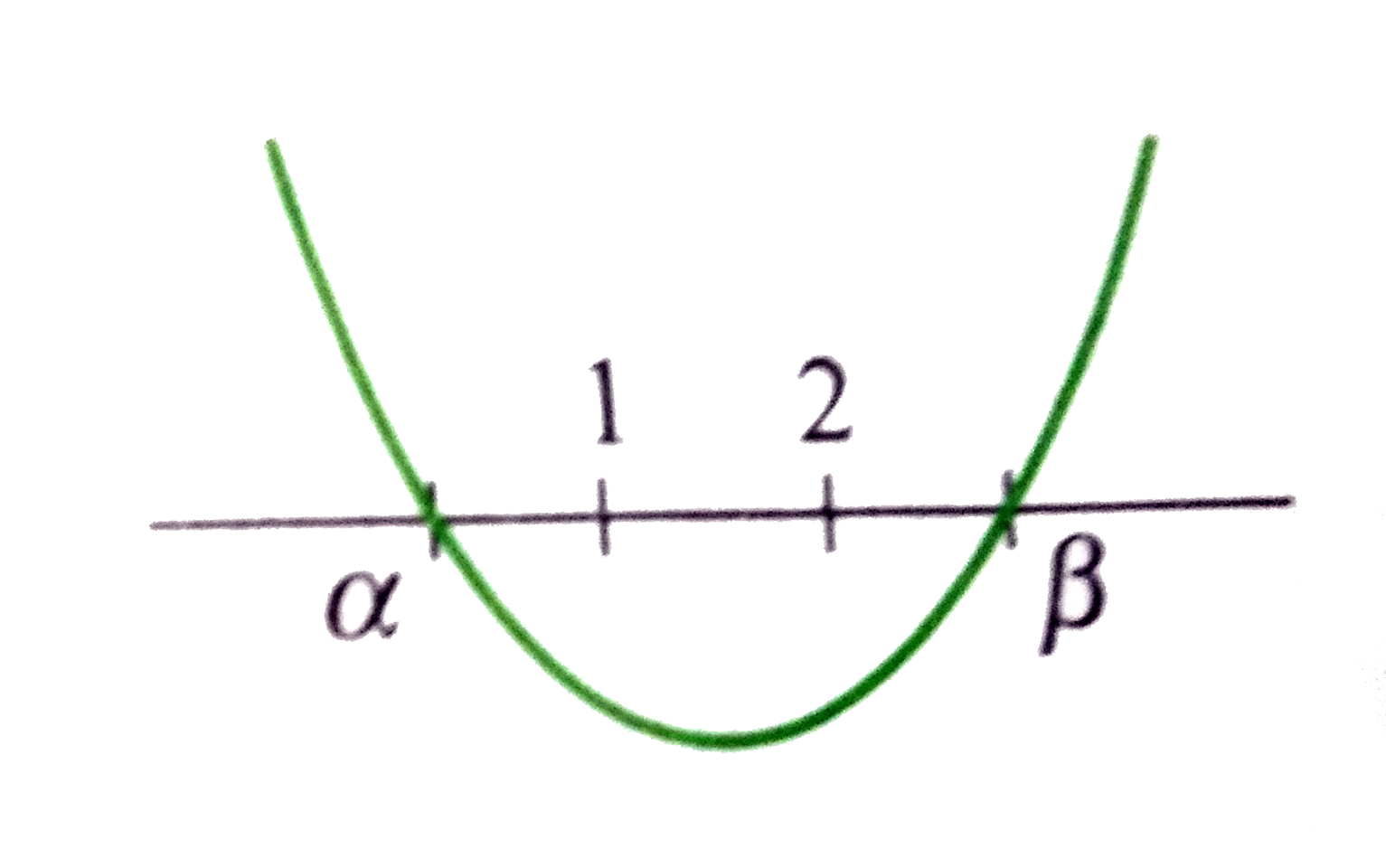
If the equation x2+2ax+a<0∀x∈[1,2], the find the values of a.Solution in Tamil
Given ,
x2+2ax+a<0.∀x∈ [1, 2]
Hence, 1 and 2 lie between the roots of the equation
x2+2ax+a=0
⇒f(1)<0andf(2)<0
⇒1+2a+a<0,4+4a+a<0
⇒a<−13,a<−45
⇒a∈(−∞,−45)
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise 2.13videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise 2.25videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer6videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year4videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank12videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
If x=1andx=2 are solutions of equations x3+ax2+bx+c=0anda+b=1, then find the value of b.
04:11View SolutionGiven that the expression 2x3+3px2−4x+p hs a remainder of 5 when divided by x+2 , find the value of p.
04:10View SolutionIf c≠0 and the equation p/(2x)=a/(x+c)+b/(x−c) has two equal roots, then p can be (√a−√b)2 b. (√a+√b)2 c. a+b d. a−b
02:56View Solutionabout to only mathematics
02:52View SolutionThe equation of the plane which has the property that the point Q(5,4,5) is the reflection of point P(1,2,3) through that plane, is ax+by+cz=d where a,b,c,d∈N. Find the least value of (a+b+c+d).
08:05View SolutionFor which values of 'a' so that the equation x2+(3−2a)x+a=0 has exactly one root in the interval (−1,2)
01:31View SolutionIf the equation asinx+cos2x=2a−7 possesses a solution, then find the value of a.
03:03View SolutionIf the function f(x)=x2−(A+2)x+Ax−2,forx≠2andf(2)=2, is continuous at x=2, then find the value of A.
04:33View SolutionLet a>2 be a constant. If there are just 18 positive integers satisfying the inequality (x−a)(x−2a)(x−a2)<0, then find the value of a.
03:43View SolutionLet a>2 be a constant. If there are just 18 positive integers satisfying the inequality (x−a)(x−2a)(x−a2)<0, then find the value of a.
04:20View SolutionIf the equation (a−5)x2+2(a−10)x+a+10=0 has roots of opposite sign, then find the value of a.
02:58View SolutionFind the greatest value of f(x)12ax−x2−5a2∈[−3,5] depending upon the parameter a.
07:21View SolutionIf x2+2ax+a<0∀x∈[1,2], the find the values of a.
02:34View SolutionForm the differential equation corresponding to y2−2ay+x2=a2 by eliminating a.
02:07View SolutionIf the equation asinx+cos2x=2a−7 possesses a solution, then find the value of a.
03:20View SolutionIf the function f(x)=x2−(A+2)x+Ax−2,forx≠2andf(2)=2, is continuous at x=2, then find the value of A.
05:25View Solution
