Question

Find the value of $\text{'}a\text{'}$ for which $a{x}^2+(a-3)x+1<0$ for at least on positive real x.

Explanation

Let `f(x) = ax^(2) + (a - 3) x + 1`
Case I:
If a `gt` 0, then `f(x)` will be negative only for those value of x which lie between the roots . From the graphs, we can see that f(x) will be less then zero for at least one positive real x, when f (x) = 0 has distinct roots and at least one of these roots is positive.
Since f(0) = 1 `gt` 0, the possible grapha according to the question is shown in the figure. From the graph, we can see that both the roots are non-negative . For this
(i) `D gt 0 rArr (a - 3)^(2) - 4a gt0`
`rArr a lt 1 or a gt 9` (1)
(ii) sum ` gt 0` and product `ge0`
`rArr (-(a-3))/(a) gt 0 or (a- 3)/(a) lt 0 and 1//a gt 0`
`rArr 0 lt a lt 3` (2)
From (1) and (2), we have
a `in (0, 1)`

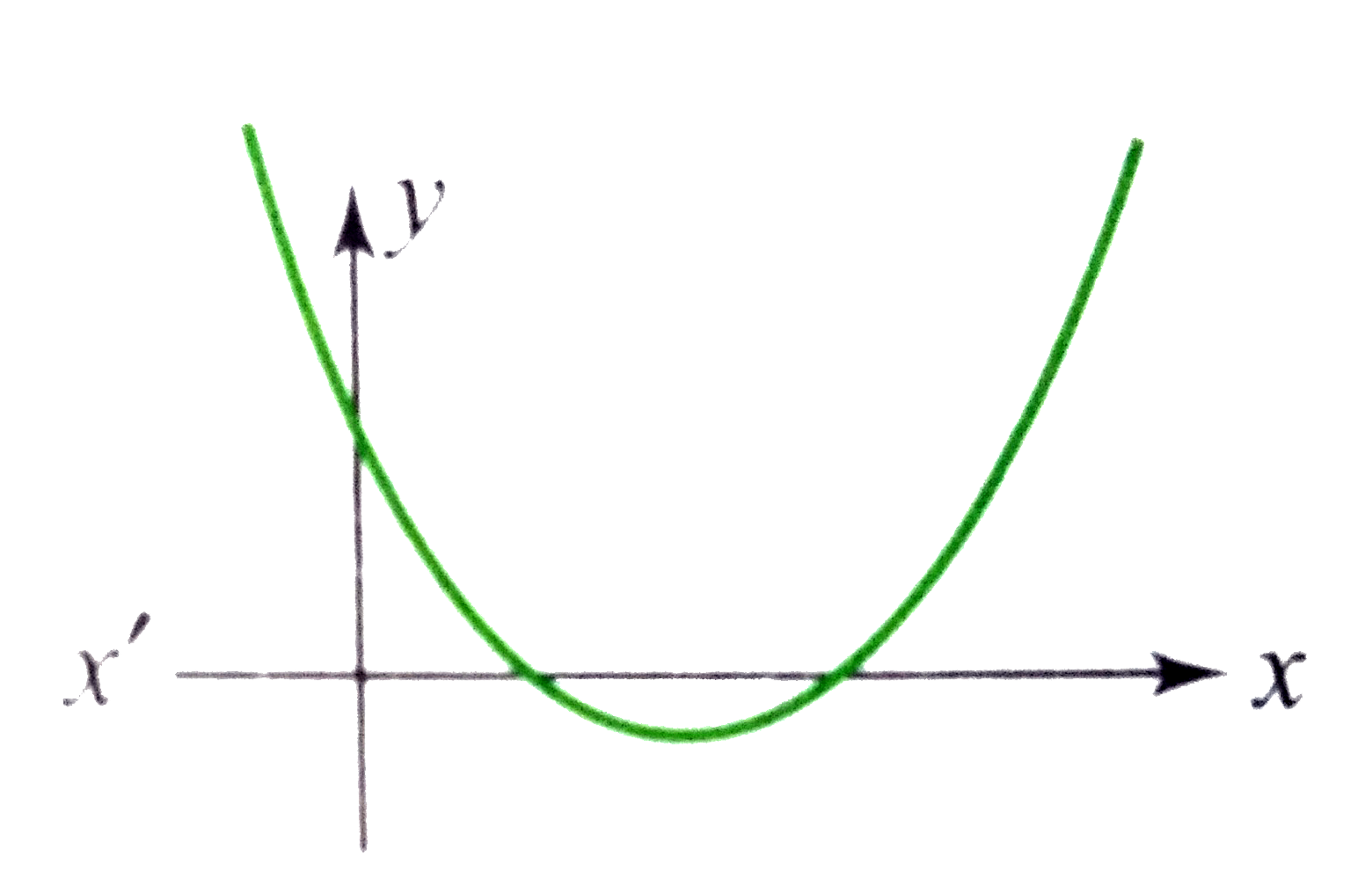
Case II : a `lt`0

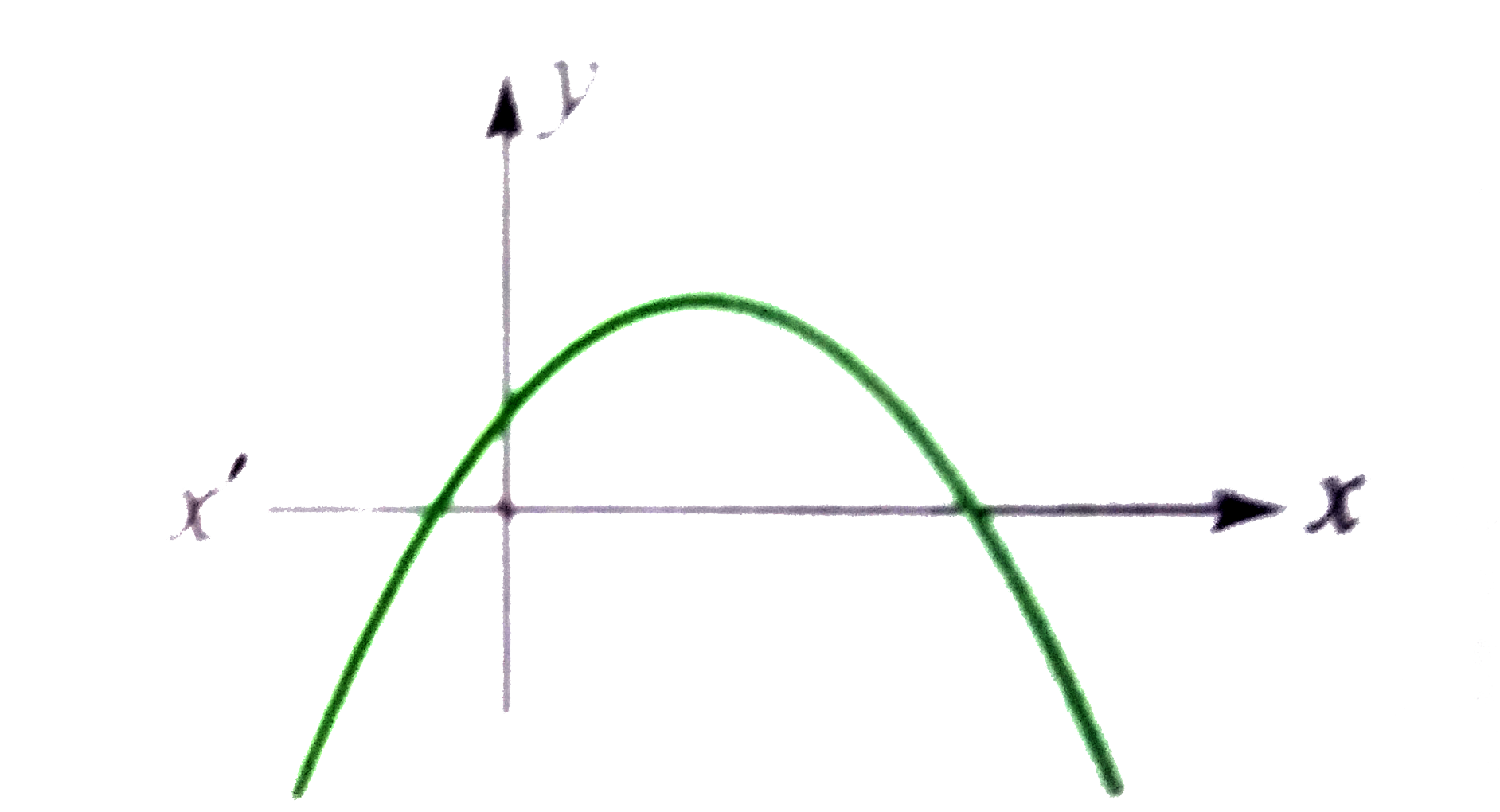
Since `f(0) = 1 gt 0,` then graph is as shown in the figure, which shows that `ax^(2) + (a - 3) x + 1 lt` 0, for at least one positive x .
Case III : a = 0
If a = 0,
f(x) = - 3x + 1
`rArr f(x) lt 0, AA x gt 1//3`
Thus, from all the cases, the required set of values of a is ` (-infty , 1)` .