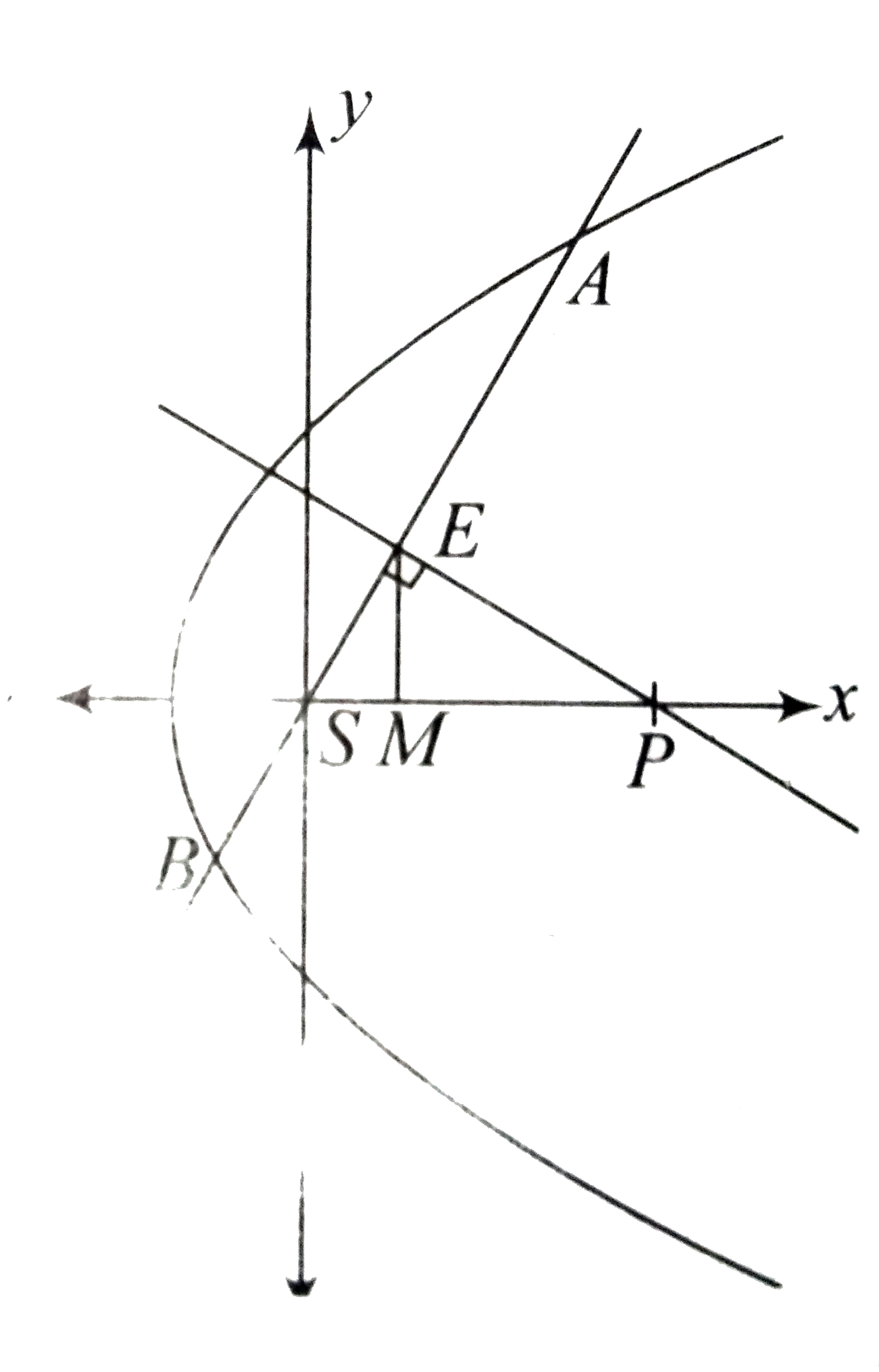
is drawn through focus S of the parabola . If two intersection points of the given line and the parabola are A and B such that perpendicular bisector of AB intersects the x-axis at P then length of PS is Solution in Tamil
The correct Answer is:D
Thus, focus is (0,0)
So, line is . Solving this line with parabola,
i.e.,
So, x-coordinate of E is .
.
Topper's Solved these Questions
- PARABOLABook:CENGAGEChapter:PARABOLAExercise:Multiple Correct Answers Type
Explore 10 Videos
- PARABOLABook:CENGAGEChapter:PARABOLAExercise:Comprehension Type
Explore 1 Video
- PARABOLABook:CENGAGEChapter:PARABOLAExercise:JEE Advenced Single Answer Type
Explore 18 Videos
- PAIR OF STRAIGHT LINESBook:CENGAGEChapter:PAIR OF STRAIGHT LINESExercise:Exercise (Numerical)
Explore 5 Videos
- PERMUTATION AND COMBINATIONBook:CENGAGEChapter:PERMUTATION AND COMBINATIONExercise:Question Bank
Explore 4 Videos
Similar Questions
A family of curve S is given by S≡x2+2xy+y2−4x(1−λ)−4y(1+λ)+4, then S=0 represents
View SolutionA parabola is drawn through two given points A(1,0) and B(−1,0) such that its directrix always touches the circle x² + y^2 = 4. Then, The locus of focus of the parabola is=
View Solutionabout to only mathematics
View SolutionThe distance between the lines (x+7y)2+4√2(x+7y)−42=0 is_____________
View SolutionIf the number of ways in which a selection of 100 balls can be made out of 100 identical red balls, 100 identical blue balls and 100 identical white balls is
View SolutionA circle is drawn having centre at C(0,2) and passing through focus (S) of the parabola y^(2)=8x, if radius (CS) intersects the parabola at point ,then
View SolutionThe line y=x-2 cuts the parabola y^(2)=8x in the points A and B. The normals drawn to the parabola at A and B intersect at G. A line passing through G intersects the parabola at right angles at the point C,and the tangents at A and B intersect at point T.
View Solutiony=√3x+λ is drawn through focus S of the parabola y2=8x+16. If two intersection points of the given line and the parabola are A and B such that perpendicular bisector of AB intersects the x-axis at P then length of PS is
View SolutionThe straight lines y=±x intersect the parabola y2=8x in points P and Q, then length of PQ is
View Solutionसरल रेखाएँ y=±x परवलय y2=8x को बिंदुओं P व Q में प्रतिच्छेद करती है, तो PQ की लम्बाई है :
View SolutionThe locus of point of intersection of any tangent to the parabola y2=4a(x−2) with a line perpendicular to it and passing through the focus, is
View SolutionA circle is drawn having centre at C(0,2) and passing through focus (S) of the parabola y2=8x, if radius (CS) intersects the parabola at point P, then
View Solutiony=√3x+λ is drawn through focus S of the parabola y2=8x+16. If two intersection points of the given line and the parabola are A and B such that perpendicular bisector of AB intersects the x-axis at P then length of PS is
View Solutionमाना वृत्त x2+y2=9 तथा परवलय y2=8x है। यह प्रथम तथा चतुर्थ चतुर्थाश में क्रमशः P तथा Q पर प्रतिच्छेद करते है। वृत्त की P तथा Q पर स्पर्श रेखाएं x-अक्ष को R पर प्रतिच्छेद करती है तथा परवलय की P तथा Q पर स्पर्श रेखा x-अक्ष को S पर प्रतिच्छेद करती है।
त्रिभुज PRS के परिवृत्त की त्रिज्या है-
View Solutionमाना वृत्त x2+y2=9 तथा परवलय y2=8x है। यह प्रथम तथा चतुर्थ चतुर्थाश में क्रमशः P तथा Q पर प्रतिच्छेद करते है। वृत्त की P तथा Q पर स्पर्श रेखाएं x-अक्ष को R पर प्रतिच्छेद करती है तथा परवलय की P तथा Q पर स्पर्श रेखा x-अक्ष को S पर प्रतिच्छेद करती है।
त्रिभुज PQR के अन्तःवृत्त की त्रिज्या है-
View Solution

